「どうして箱ひげ図は外れ値を見つけやすいの?」
「外れ値と異常値ってどう違う?」
と、気になりますよね。
箱ひげ図では、一般的に第1四分位数から四分位範囲の1.5倍以上離れた値、または第3四分位数から四分位範囲の1.5倍以上離れた値を外れ値として、箱ひげ図のひげの外側に小さな点や丸で表示されます。
そのため外れ値が非常に見つけやすく、初期段階で「異常なデータ(外れ値)」に気づくことができます。
この記事ではさらに詳しく、
- 箱ひげ図の外れ値を扱うときの注意点2つ
- 箱ひげ図で外れ値を判定する3つの手順
についてお伝えしていきます。ぜひ参考にしてみてください。
目次
箱ひげ図の外れ値とは
箱ひげ図(ボックスプロット)は、データの分布・中央値・ばらつき・外れ値を視覚的に表す統計グラフです。
そして、外れ値とは、データの中で他の値から大きく外れた極端に小さな値、あるいは極端に大きな値のことを指します。
外れ値は統計的に「異常な値」とみなされ、箱ひげ図では通常、ひげの範囲外に小さな点や丸として描かれるのが一般的です。
箱ひげ図の基本的な見方
まず、箱ひげ図の基本的な見方について解説していきます。
箱ひげ図は、「5数要約」と呼ばれる以下の5つの数値を使ってデータの分布を可視化します。
- 最小値: 外れ値を除いたデータの中で最も小さい値
- 第1四分位数(Q1): データを小さい順に並べたとき、全体の25%の位置にくる値
- 中央値・第2四分位数(Q2):データを小さい順に並べたとき、 データの中央(全体の50%)にくる値
- 第3四分位数(Q3) :データを小さい順に並べたとき、全体の75%の位置にくる値
- 最大値 :外れ値を除いたデータの中で最も大きい値
四分位数とは、小さい順に並べたデータを4等分する際の3つの区切り値(25%/50%/75%)のことです。
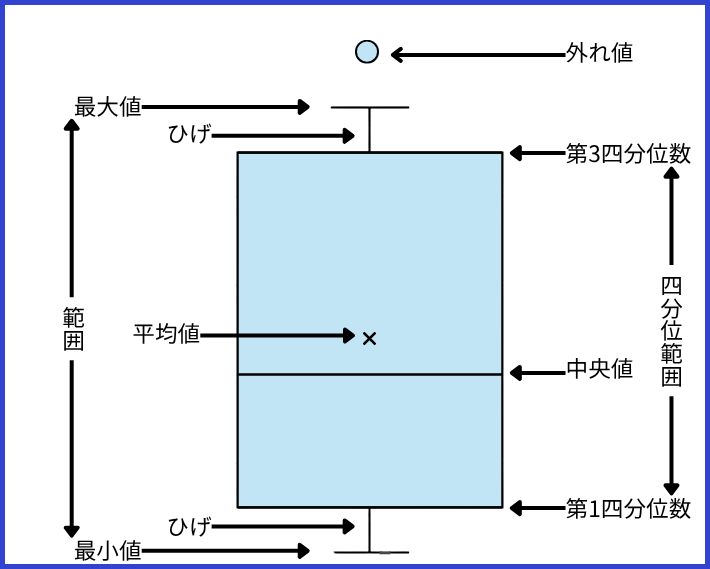
また、Q3からQ1を引いた値を四分位範囲(IQR)と呼び、データの中央部分50%の範囲を指します。
四分位数の求め方については、『箱ひげ図で外れ値を判定する3つの手順』の章で詳しく解説しています。
外れ値と異常値の違い
外れ値は「データの分布において他の値から極端に離れた値」であることを解説してきました。
外れ値と同じ意味で使われる用語に、異常値があります。
外れ値も異常値も、英語では「outlier」と表現するので混同されがちですが、より厳密にいうと異常値は「外れ値の中で、記入ミスや測定ミスなど値が大きく外れた原因がわかっているもの」を指します。
例えば、小学生の身長データをまとめる際に150cmを誤って1500cmと入力としていた場合は入力ミスによる異常値といえます。
上の例のように、値が大きく外れた原因が明確な異常値であれば、データから除外してしまっても問題ありません。
箱ひげ図で外れ値を扱うときの注意点2つ
外れ値は、データの質を大きく左右するため、扱う際には判断や処理に注意が必要です。
具体的な注意点として、
- 【注意点1】外れ値により分析精度が低下する恐れがある
- 【注意点2】外れ値は必ずしも除外対象ではない
の2つが挙げられるので、順に解説していきます。
【注意点1】外れ値により分析精度が低下するおそれがある
他のデータと大きくかけ離れている外れ値は、データ全体の平均や傾向をゆがませる可能性があります。
例えば、クラスのテスト点数が全体的に70〜80点の中で、1人だけ10点を取っていると、平均点が下がりすぎて実際の学力分布が正しく把握できなくなります。
平均・比率・割合などを求めたい場合には、上の例のような影響の大きい外れ値を除外することでより正確な分析結果が得られます。
ただし、次の【注意点2】で解説するように、外れ値が実際に意味のあるデータである場合もあるため、外れ値の性質をよく確認したうえで判断することが重要です。
【注意点2】外れ値は必ずしも除外対象ではない
外れ値だからといって無条件に除外するのではなく、まずは「なぜ外れ値が発生したのか」の原因を特定し、異常値なのか、もしくは重要な出来事を示している値なのかを見極めましょう。
例えば、ある店舗だけ先月の売上が他の店舗よりも突出して高く、なぜそうなったのか改めて分析した結果新しい販促施策の影響だとわかれば、他の店舗でもその施策を応用することで企業全体の売上が向上する可能性が出てきます。
新しいビジネスチャンスの発見や、異常検知・トラブルの早期発見に繋がる可能性もあるため、一概に外れ値を除外すればよいとは言い切れません。
外れ値がデータ全体にどのような影響を与えるのか、またどのように処理するべきかを理解してから、分析目的に応じた適切な処理方法を選ぶといいでしょう。
箱ひげ図で外れ値を判定する3つの手順
外れ値を正確に把握するために、正しい手順で箱ひげ図を作成しましょう。
箱ひげ図では主に、四分位範囲とひげの範囲を使って外れ値の判断を行います。
- 【手順1】四分位間の距離を計算する
- 【手順2】ひげの上下限を計算する
- 【手順3】ひげの範囲から外れた値を外れ値と判定する
箱ひげ図で外れ値を判定する方法を、上記3つの手順で解説します。
【手順1】四分位間の距離を計算する
あるクラスの小テストの点数が「0,1,1,2,3,5,8,9,9,10」だった場合を例にして見てみましょう。
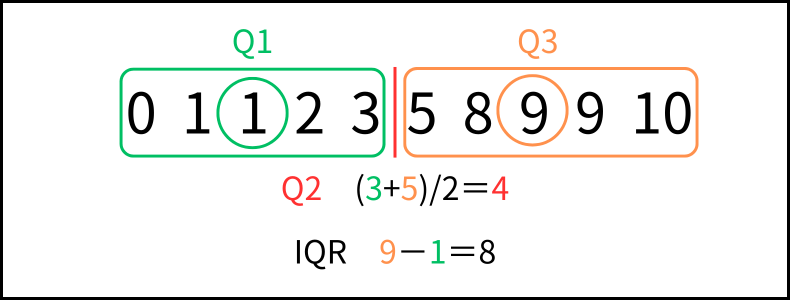
まず、データを小さい順に並べ、中央値となるQ2から求めます。
今回はデータ数が偶数個のため、「(3+5)/2」でQ2は「4」です。
Q2の次に、第1四分位数・Q1(25%)と第3四分位数・Q3(75%)を求めます。
今回の例だと、Q1は「0,1,1,2,3,」の中央値の「1」で、Q3は「5,8,9,9,10」の中央値の「9」です。
次に、『箱ひげ図の基本的な見方』の章でも触れたとおり、Q3からQ1を引いた値が四分位間範囲(IQR)なので、ここでは「9−1=8」になります。
【手順2】ひげの上下限を計算する
ひげの範囲は、下限は「Q1-1.5×IQR」、上限は「Q3+1.5×IQR」で求めます。
ここでは下限は「1-1.5×8=-11」、上限は「9+1.5×8=21」になり、-11~21の範囲外のデータが外れ値となります。
【手順3】ひげの範囲から外れた値を外れ値と判定する
箱ひげ図では基本的に、外れ値はひげの外に点や記号で表現されます。
今回のデータには、−11より小さい値も、21より大きい値もないため、外れ値はありません。

このように箱ひげ図で表すことで、外れ値が存在しないことが視覚的にもわかります。
箱ひげ図はExcel(エクセル)でも作成できる
Excelでも、以下の手順で簡単に箱ひげ図を作成することが可能です。
Excelでの箱ひげ図の作り方
【手順①】Excelのシートに、縦方向(列)にデータを入力する
【手順②】入力したセル範囲を選択し、挿入タブから統計グラフの箱ひげ図を選択
【手順③】必要に応じて見た目を調整する
Excelでの箱ひげ図の詳しい作り方については『箱ひげ図を使うメリット・デメリットや実際の作り方を解説』の記事をご参照ください。
また、Excelの箱ひげ図で外れ値を表示する設定は、通常はデフォルトで有効になっていますが、非表示になっている場合や表示方法を変更したい場合は以下の手順で設定できます。
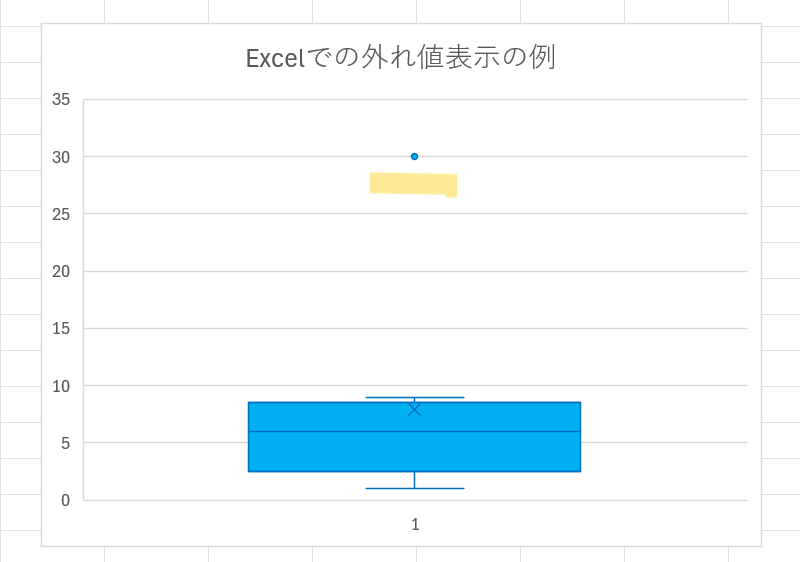
上の図は、外れ値が表示されている状態です。
【手順①】「データ系列の書式設定」を開く
グラフ上で右クリックしてから「データ系列の書式設定」を選択すると、右側に設定画面が表示されます。
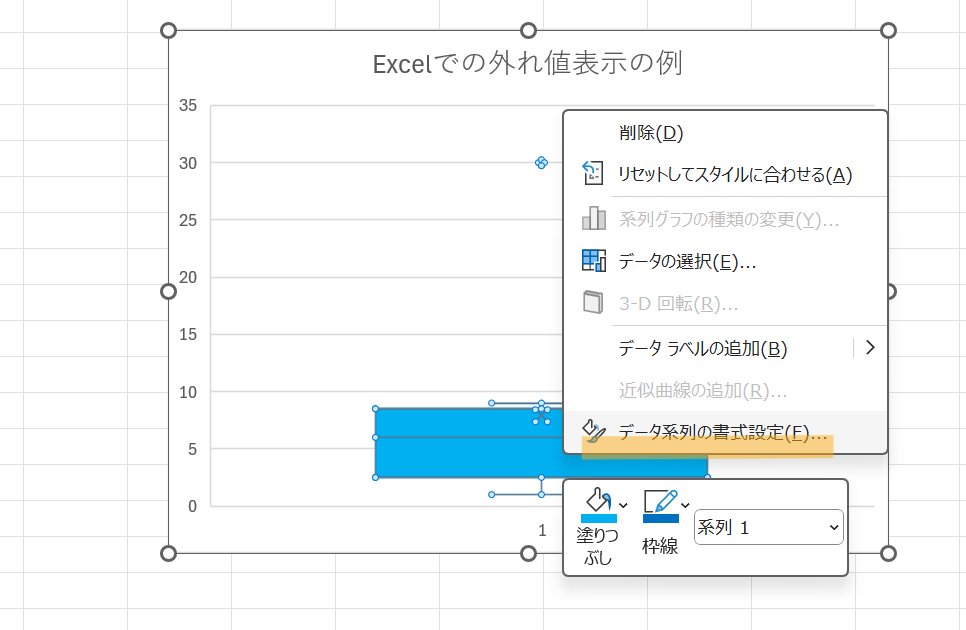
グラフの上でダブルクリックをしても、同じように「データ系列の書式設定」が表示されます。
【手順②】「特異ポイントを表示する(O)」にチェックが入っているか確認
書式設定ウィンドウの「系列のオプション」タブから、「特異ポイントを表示する(O)」を確認しましょう。
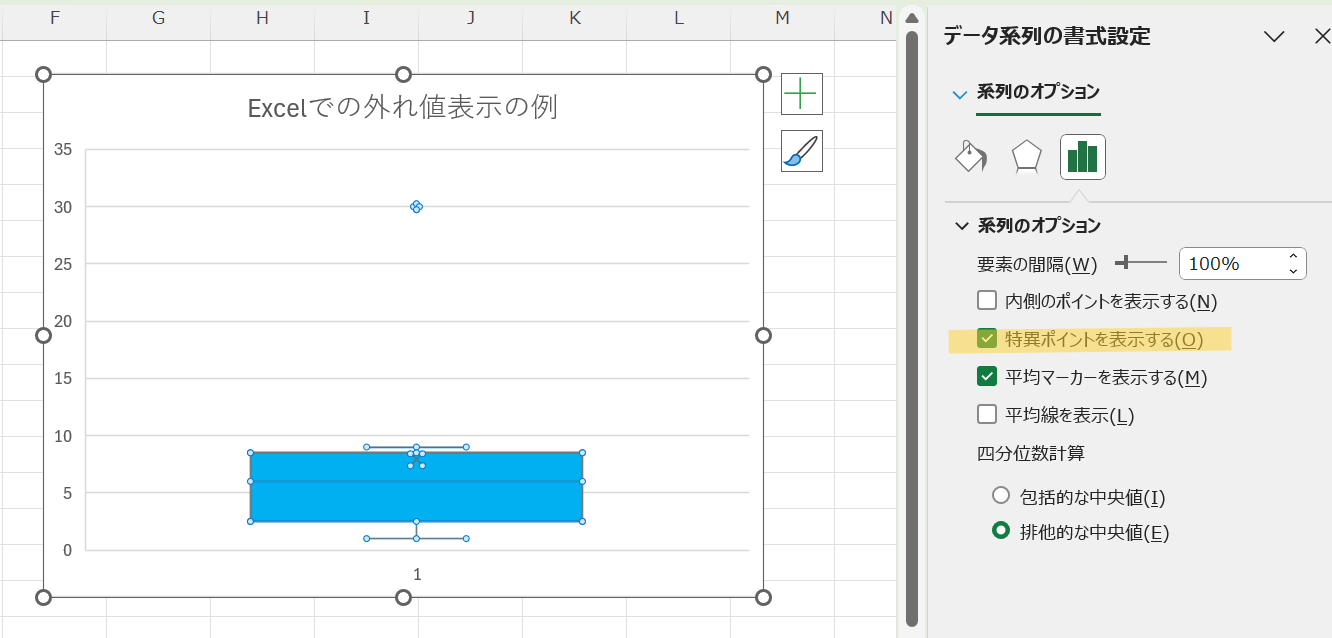
外れ値を表示したい場合はチェックを入れ、非表示にしたい場合はチェックを外します。

これで外れ値が非表示になりました。
平均マーカーや平均線も、外れ値と同じく「データ系列の書式設定」から簡単に表示・非表示を設定できます。
まとめ
今回は、箱ひげ図での外れ値の判定方法や、外れ値と異常値の違いなどを解説しました。
箱ひげ図で外れ値を扱う際は、
- 【注意点1】外れ値により分析精度が低下するおそれがある
- 【注意点2】外れ値は必ずしも除外対象ではない
上の2点に注意して、値が大きく外れた原因やデータ分析を行う目的を考慮して、外れ値を除外するかどうか慎重に判断するといいでしょう。
箱ひげ図で外れ値を判定する手順は、以下の通りです。
- 【手順1】四分位間の距離を計算する
- 【手順2】ひげの上下限を計算する
- 【手順3】ひげの範囲から外れた値を外れ値と判定する
箱ひげ図は、データの特徴や分布を把握するのに便利なグラフなので、外れ値も見つけやすいです。
新たなビジネスチャンスの発見や、異常・トラブルの早期察知につなげるために、まずはデータ分析を正しく活用することが重要です。
「もともとデータ分析が得意!」「知識に自信はないけど、統計っておもしろそう!」などなど、少しでも興味が沸いた人はかっこ株式会社のインターンに参加してみませんか?
ぜひ『データサイエンス未経験でもOK!学生3人が語るかっこのインターンの魅力とは?』の記事もご参照ください。