「標準偏差ってどうやって求めるの?」
「目安ってどのくらい?」
と、気になりますよね。
標準偏差は簡単な指標であるうえ、ビジネスや偏差値の計算など様々な場面で使用されています。
標準偏差を正しく理解し利用することで、データのばらつき具合を把握し、顧客の特徴などビジネスにとって大切な情報を得られます。
本記事では、
- 標準偏差の求め方や目安
- 標準偏差が使える場面
が分かるのでぜひ参考にしてみてください。
目次
標準偏差とは
標準偏差とは、“データの平均値からの”ばらつきや散らばり具合を表すもので、各データが平均値から大体どの程度にあるのかを表します。
例えば、ある学校の100人の生徒に2つのテストを実施し、次のような2つのグラフが得られたとします。
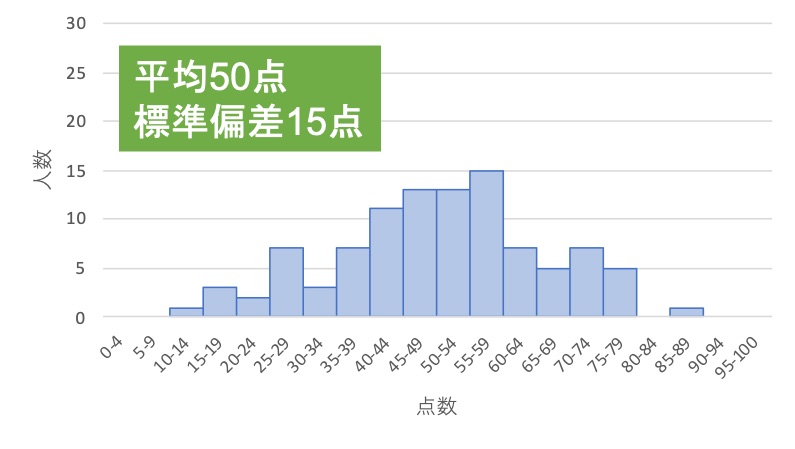
↑1つ目のテスト「標準偏差15点」
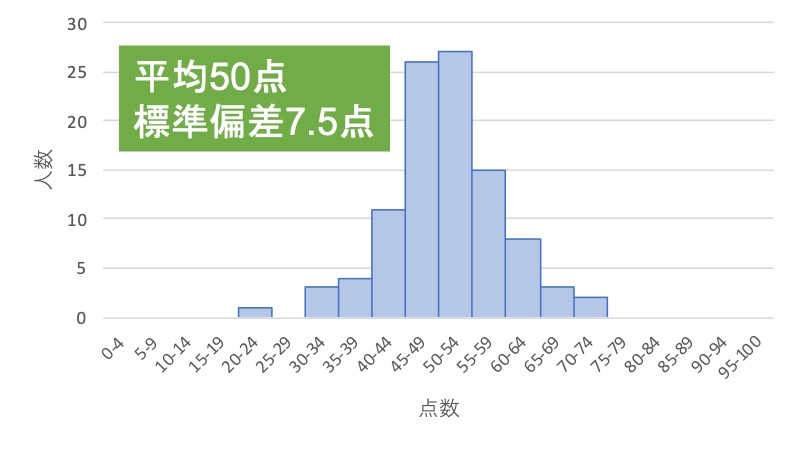
↑2つ目のテスト「標準偏差7.5点」
これらのグラフでは、平均点は「50点」と同じですが、標準偏差が「15点」と「7.5点」で異なっています。
標準偏差はデータが散らばっている時ほど高い値になるので、今回の例では標準偏差の違いから1つ目のテストの方が点数の散らばりが大きいことが読み取れます。
このように、標準偏差はデータの散らばり具合を把握してデータの特徴を掴むことに用いられるのです。
「偏差値」で分かる「標準偏差」の便利さ
「標準偏差」が便利であることを「偏差値」を参考に説明していきます。
偏差値は「データの中でどれくらいの位置にいるか」を表す指標で、標準偏差と平均を使って計算するため偏差値を出すことで、どちらのテストで高い点を取ることがすごいのかを知れます。
先ほどのテストの例を参考に「2つのテストの60点の価値」を推し量ります。
1つ目のテストでは、平均点から±15点のズレが標準的です。
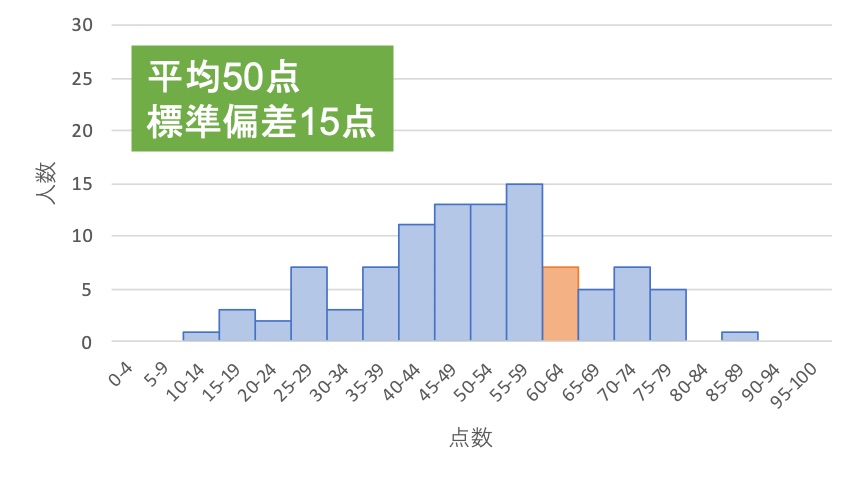
↑1つ目のテストで60点
2つ目のテストでは、平均点から±7.5点のズレが標準的です。
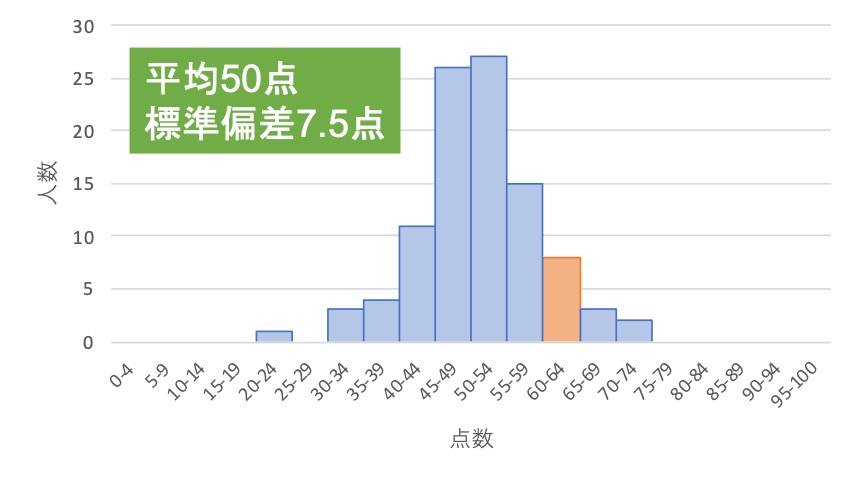
↑2つ目のテストで60点
この情報だけだと、A君は2つのテストで同じ成績を収めたように思えます。 しかし、平均点と収めた点数が同じだとしても、「偏差値」によってこの60点が表す成績の良さは異なります。
それぞれの「標準的」の範囲に比べてどれくらい高い点を取ったかを考えると、どちらのテストで高い点を取ることがすごいのかが分かります。
この考え方で算出される値が「偏差値」なのです。
学力を表す偏差値は、50を基準とすることが普通なので、平均点を取れば偏差値は50となります。
ちなみに、1つ目ののテストで60点を取った場合の偏差値は56.7で、2つ目のテストで60点を取った場合の偏差値は63.3になります。2つ目のテストで60点を取った場合の方が優秀であることが分かります。
標準偏差が使える3つの場面

標準偏差はデータの特徴を掴めることから、ビジネスや学校などさまざまな場面で使われています。
この標準偏差が使える場面は主に以下3つの場面です。
- ロイヤルカスタマーを見つけ出したい時
- Webサイトのアクセス数の異常を検知する時
- 自分の学力がどのくらいか把握したい時
それぞれ解説していきます。
ロイヤルカスタマーを見つけ出したい時
ロイヤルカスタマーを見つけ出したい時に標準偏差が用いられます。
ロイヤルカスタマーとは、多くの商品を購入してくれ自社に信頼を寄せてくれている顧客のことです。
企業にとって、ロイヤルカスタマーがどれだけ離れないようにするかは重要な問題です。
標準偏差を用いることで、購買金額の平均値+標準偏差を超える金額を支払ってくれている顧客(ロイヤルカスタマー)を見つけ出すことができます。
グラフに表すと以下のようになります。
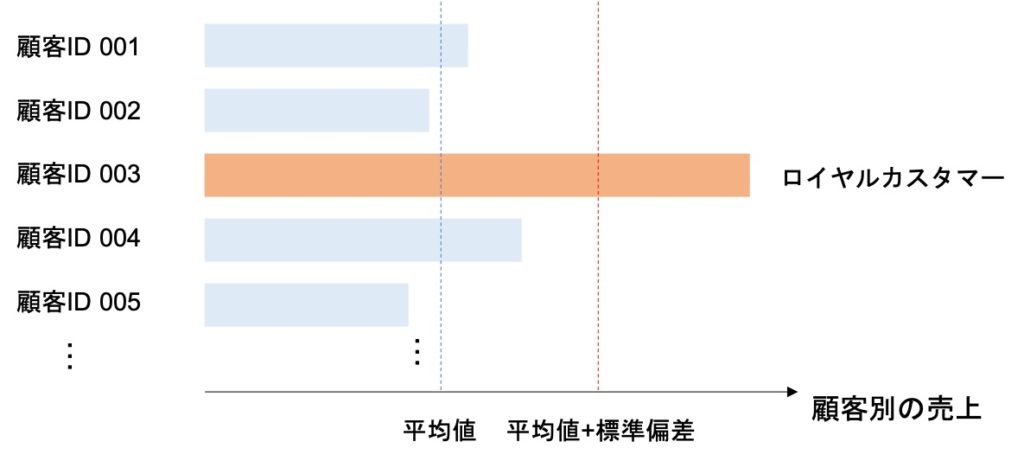
このように、それぞれの顧客に対して平均値+標準偏差の金額を超えているか超えていないかを見える化することができます。
その結果、ロイヤルカスタマーになる人の特徴を分析し、ロイヤルカスタマーの新規獲得に向けた施策を考えることもできます。
Webサイトのアクセス数の異常を検知する時
Webサイトのアクセス数の異常を検知する時にも標準偏差が重要になります。
Webサイトのアクセス数の異常を検知できなければ、もし自社のサイトが攻撃を受けていたとしても把握できない状態になります。
標準偏差を用いることで、アクセス数の異常を検知できるようにすることで、サイトのダウンや障害を防げるのです。
こちらもグラフに表してみましょう。
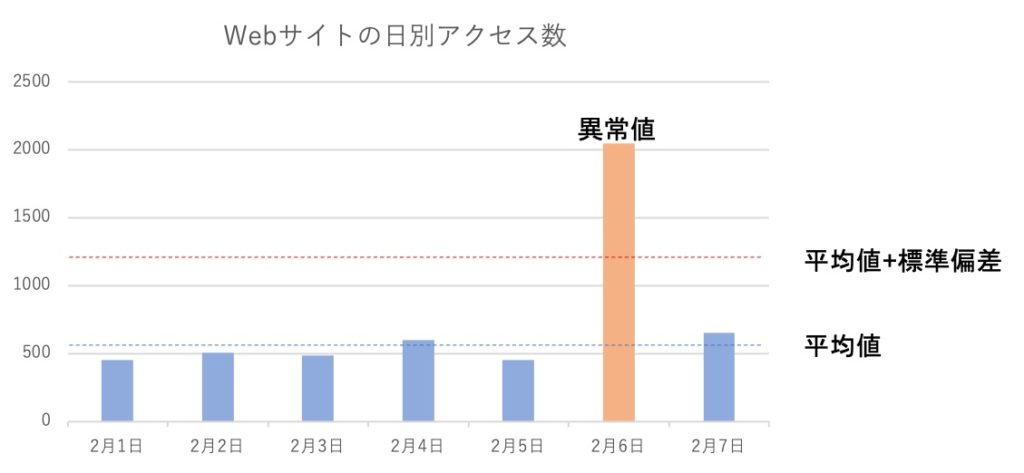
このように平均値+標準偏差にしきいを設けておくと、2月6日が異常な値になっていることが読み取ることができます。
その結果、異常なアクセスの原因を特定するために分析を行うことなどが可能です。
自分の学力がどのくらいか把握したい時
学校のテストで自分の学力がどの程度に位置しているのかを調べることにも標準偏差が使えます。
例えば、あなたが60点のテストの点数の分布が以下のグラフであったとします。

もし、標準偏差を知らなければ、平均点が50点であなたの点数が60点のため、そこまでよい点数ではないれいとsと考えてしまいます。
しかし、標準偏差が7.5であると求めることで、あなたの点数は57.5点(平均値+標準偏差の点数)より高いことが分かり、良い点数なのだと自信を持てます。
このように、自分の学力を客観的に判断するために標準偏差が用いられます。
学力の指標として偏差値がありますが、偏差値の計算にも標準偏差が使われています。
標準偏差の求め方4ステップ
標準偏差が使える場面について知ったところで、標準偏差の求め方に移りましょう。
標準偏差は次のような公式になります。
\[ 標準偏差(\sigma) = \sqrt{(\sum_{i=1}^{n}(x_i – \mu)^2) \div n} \]
この式を求めるために以下の4ステップを踏みます。
- データの平均値を求める
- データ点と平均値の差(偏差)を求める
- データの分散を求める
- データの標準偏差を求める
これらのステップを踏めば、簡単に標準偏差を求めることができます。
それぞれ解説していきます。
STEP1. データの平均値を求める
まず、データの平均値を求めましょう。
標準偏差の公式では、\( \mu \)が平均値を示す定数です。
\[ 平均値(\mu) = (\sum_{i=1}^{n}x_i) \div n \]
上記の式のように、データの全ての値を合計し、データの数で割ることで平均値を求めます。
STEP2. データ点と平均値の差(偏差)を求める
平均値を求めたら、その平均値を使って偏差を求めます。
偏差とは、データ点と平均値との差のことです。
\[ 偏差 = x_i – \mu \]
上記の式は1つのデータ点に対する偏差です。
偏差は次の分散の式で用います。
STEP3. データの分散を求める
データの分散は、偏差を二乗して平均を求めることで算出します。
偏差を二乗するのは、偏差は各データ点から平均を引いていることで合計すると0になってしまうためです。
二乗することですべての値を正の値にして、合計しても0にならないようにするのです。
\[ 分散(\sigma^2) = (\sum_{i=1}^{n}(x_i – \mu)^2) \div n \]
上記の式が分散の式です。
ここまで求めたらあと少しです。
STEP4. データの標準偏差を求める
分散の平方根を求めることで、データの標準偏差を計算します。
平方根とは二乗の逆の操作で、分散の計算で二乗した部分を打ち消す操作を標準偏差の計算で行います。
\[ 標準偏差(\sigma) = \sqrt{(\sum_{i=1}^{n}(x_i – \mu)^2) \div n} \]
冒頭で示したように標準偏差の式にたどり着きました。
それぞれの変数に値を入れれば標準偏差が求まります。
標準偏差をエクセルで求める方法
標準偏差はエクセルで簡単に求められます。
標準偏差の求め方4ステップで示したように、標準偏差の計算には二乗や平方根を求めるところがあり、大量のデータの標準偏差を手計算で求めることは難しいです。
そのため、エクセルなどのツールでは標準偏差を求めるための関数が用意されています。
エクセルの関数は主に2つです。
- STDEV.P関数
- STDEV.S関数
どちらを使うかで標準偏差の値が大きく変わります。
それぞれ解説します。
STDEV.P関数を用いる方法
STDEV.P関数は調べたいデータがすべて揃っている場合の標準偏差を求める関数です。
例えば、学校で行ったテストの標準偏差が知りたいとして、生徒の点数のデータがすべて手元にあれば、STDEV.P関数を用います。
=STDEV.P(対象となる範囲を選択)
で標準偏差を求められます。
STDEV.S関数を用いる方法
STDEV.S関数は、調べたいデータの一部しか手元にない場合に調べたいデータ全体の標準偏差を求める関数です。
例えば、全国規模のテストの標準偏差を知りたいのに、あなたの学校で行ったテストの点数のデータしか手元にない場合に用います。
=STDEV.S(対象となる範囲を選択)
で全体のデータの標準偏差が求められます。
どちらの関数を使うかによって大きく結果が変わることがあるため、注意しましょう。
まとめ
標準偏差は、データのばらつきや散らばり具合を表すものです。
標準偏差を求めることで役に立つ場面は多くあります。
この記事では例として以下の3つを取り上げました。
- ロイヤルカスタマーを見つけ出したい時
- Webサイトのアクセス数の異常を検知する時
- 自分の学力がどのくらいか把握したい時
平均値±標準偏差の値は特殊な値であるため、異常な値であると判断でき、ロイヤルカスタマーやアクセス数の異常を検知できます。
標準偏差は以下の4STEPで求められます。
- データの平均値を求める
- データ点と平均値の差(偏差)を求める
- データの分散を求める
- データの標準偏差を求める
標準偏差の公式を覚えるだけでなく、公式にたどり着くまでの流れまで把握するようにしましょう。
ビジネスシーンにおいては標準偏差をエクセルなどのツールを用いて計算します。
エクセルの関数は以下の2つです。
- STDEV.P関数
- STDEV.S関数
これらの関数はそれぞれ、状況によって使い分けることが必要です。
もし自社で、「標準偏差などのさまざまな指標から顧客の特徴を掴みたい…」「そもそもデータをどのように扱っていいか分からない…」というお悩みがあれば、『かっこのデータサイエンス』にお問合せください。
状況のヒアリングを行い、お持ちのデータから顧客分析や課題点の洗い出しを行います。
サンプルデータの確認や課題の洗い出しまで無料で承っていますのでお気軽にご相談ください。(※データの集計や本データの分析、改善の実施には費用がかかります。)
詳細は以下のページからご確認ください。