「なんでも平均でいいの?」
「平均値や中央値ってどう使い分けるの?」
と気になりませんか?
子どもの頃から馴染みがあって、使いやすいため「平均」という言葉は日常のいたるところで見かけます。
しかし、データ全体の特徴を分かりやすく見るために使われる代表値には、「平均値」以外に「中央値」「最頻値」といった種類があります。
代表値を適切に扱えると、データ分析の前に行うデータの特徴把握が効率的に行えます。
本記事では、
- そもそも代表値とは
- 平均値や中央値、最頻値の使い分け
についてお伝えしていきます。ぜひ参考にしてみてください!
\経験豊富なかっこのデータサイエンティストがまとめました!/ 
目次
なんでも平均でいいの?適切な代表値とは
「なんでも平均でいいの?」の結論から言うと、なんでも平均ではいけません。
世の中には平均値では特徴を掴めないデータがあり、中央値や最頻値と適切に使い分ける必要があります。
そもそも、データの代表値とは、大量にあるデータの特徴を簡単に理解するために用いられる値です。
データの特徴を把握できる値であることから、データ同士の比較を行う際にも用いられ、実務では最初の分析の方針を立てる時のデータの特徴を把握するために代表値が算出されます。
代表値の3つの種類
代表値には以下の3つの種類があります。
- 平均値
- 中央値
- 最頻値
代表的な値として平均値がありますが、平均値だけではデータの本来の特徴を捉えられないことがあります。
平均値だけでデータの特徴を掴めない時に用いるのが、中央値と最頻値です。
以下では、架空のA社とB社の会社員の年収をまとめた表とヒストグラムを用いてそれぞれの数値を説明します。
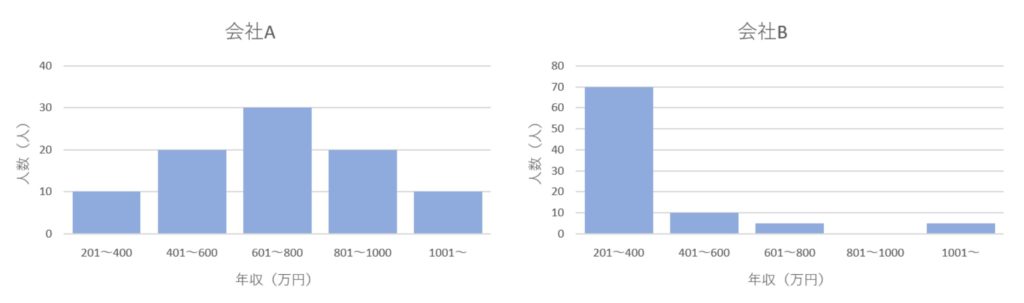
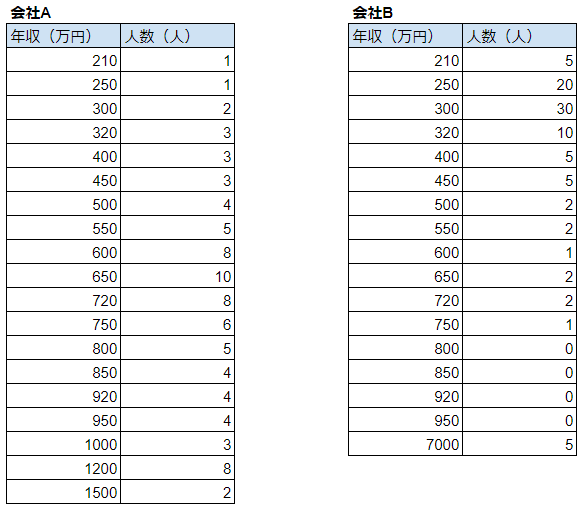
会社A、会社Bの年収と人数の内訳は、上図の通りです。
それぞれ解説していきます。
①平均値
平均値とは全てのデータを足し合わせ、データの合計をデータの個数で割った値です。
平均年収や平均身長など日常のさまざまな場面でデータの中心的な値を知るために平均値が用いられています。
例えば、「1,2,3,4,10」と5つの数字の平均値を求めると、20(5つの数字の合計) ÷ 5(データの個数) = 4(平均値)となります。

上図の年収の例から、平均値がデータの特徴を掴みきれない可能性があることを見ていきましょう。
会社Aと会社Bの年収の平均を算出してみると、以下のようになります。
- 会社Aの年収の平均値:約682万円
- 会社Bの年収の平均値:約708万円
もし、あなたが年収の多い会社に入りたいと考えていた時、「年収の平均値が会社Bの方が大きいから、会社Bに入ろう」と考えますよね。
しかし、平均値だけを判断材料として会社Bに入社しても、年収が上がらない可能性があります。
会社Bの年収のデータの分布をヒストグラムで見てみましょう。

会社Bには、年収7,000万円の人が5人いることで、平均値を底上げされていたことが分かります。
このように、平均値は全ての値で計算するため、極端な数値(例では年収7,000万)が入っているとその値に影響されてしまうのです。
そのため、平均値を求めるときには極端な値(外れ値)がないか注意する必要があります。
②中央値
中央値とは数値を小さい方から順に並べたときに真ん中に位置する値です。
平均値と異なり、ちょうど真ん中の値を中央値とするため、極端な値(外れ値)の影響を受けない特徴があります。
7つの数値を「1,2,3,4,5,6,1000」と小さい順に並べて、平均値と中央値を比較してみましょう。
- 平均値:146
- 中央値:4番目の数値である4
平均値を計算すると約146となり、1000という値に引っ張られていますが、中央値は4となり1,000の影響を受けていません。
このように極端な値(外れ値)がある場合には、平均値ではなく中央値を用いなくてはなりません。
では、年収の例でも中央値を考えていきます。
- 会社Aの年収の中央値:720万円
- 会社Bの年収の中央値:300万円
会社Bでは年収7000万円の人がいたことで平均値が引き上げられていました。
中央値で2社を比較することで、平均値だけでは見えてこなかった会社Bの年収が低さが見て取れます。

ですが、中央値だけを算出して平均値は算出しなくてよいと勘違いしてはいけません。
例えば、会社Aが、年収850万円以上の人たちを全員800万円に減俸しても、中央付近のデータの順番が変化していないため、中央値は720万円のままになってしまいます。
このように、中央値はデータの真ん中だけを表しているため、中央値以外のデータの変化を把握できないということに注意しましょう。
③最頻値
最頻値とは一番個数が多い値です。
最頻値はデータのなかで最も個数が多い値を示しているため、大多数のデータの値を知りたい時に役に立ちます。
例えば、数値が「1,2,3,3,3,4,5,5,1000」とあったとき、最頻値は3になります。

上図の年収の例では、最頻値はそれぞれ以下の数値になります。
- 会社Aの最頻値:650万円
- 会社Bの最頻値:300万円
最頻値も中央値と同じく極端な値(外れ値)の影響を受けず、最頻値からも会社Bの年収が低い事が確認できます。
しかし、最頻値にもデメリットがあります。

極端な例ですが、それぞれの金額帯の年収の人数が同じだった場合、1番個数が多いものがなくなるため、最頻値がなくなってしまいます。
また、そもそもデータの数が少ない場合、正しい結果が得られない可能性がある点にも注意しましょう。
代表値の選び方・使い分け方2ステップ

どの代表値を使うのかを判断するために、以下の2ステップを行いましょう。
- ヒストグラムを作成する
- ヒストグラムの分布から代表値を選ぶ
ヒストグラムを見ることで、データの分布や極端な値(外れ値)の有無を確認できます。
そのため、代表値の選択はヒストグラムを見て判断します。
まず、ヒストグラムの見方や作成方法について詳しく知りたい方は『ヒストグラムとは?見方やエクセルでの作り方・経営分析の例を解説』の記事をご参照ください。
では、それぞれのステップを解説していきます。
STEP1. ヒストグラムを作成する
データの分布を把握するためのグラフであるヒストグラムを作成します。
どの代表値を選ぶのかを判断するためにデータの分布を把握します。
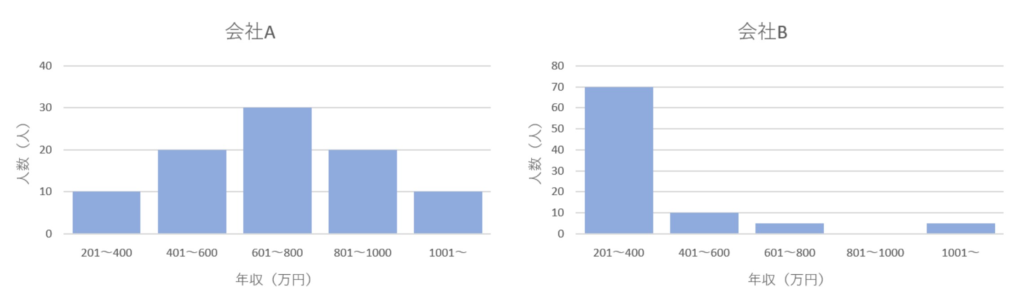
年収の例で取り上げた上の画像のような2つのグラフが会社Aの会社Bの年収の分布を見える化したヒストグラムになります。
データの分布で注目するのは分布の形と極端な値(外れ値)がないかです。
また、棒の範囲を適切に調整し、正しく分布を表せているかを確認しましょう。
STEP2. ヒストグラムの分布から代表値を選ぶ
ヒストグラムを作成できれば、データの分布を確認します。
データの分布は以下の2つに分類できます。
- きれいな山型の分布
- きれいではない分布
この2つに分類できれば、代表値を使い分けることができます。
それでは、会社Aと会社Bの年収のヒストグラムを上記のように分類してみましょう。

会社Aと会社Bの分布はそれぞれ以下のように分類できます。
- 会社A:きれいな山型の分布
- 会社B:きれいではない分布
1つの山のようになっている分布がきれいな山型の分布、それ以外をきれいではない分布と分類します。
以下からは、それぞれの分布での代表値の選び方を解説していきます。
きれいな山型の分布の場合
きれいな山型の分布である場合、代表値は平均値を採用します。
きれいな山型の分布では、平均値や中央値・最頻値は似た値になるためです。
会社Aの年収の分布がきれいな山型の分布です。
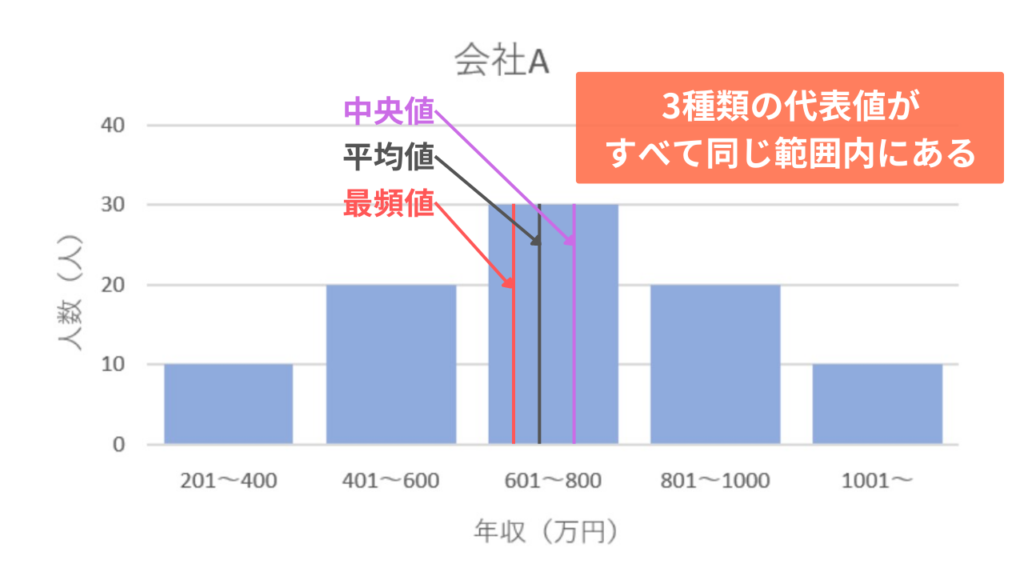
上図のように、会社Aの平均値・中央値・最頻値はすべて600~800万円の範囲に入っています。
このように、3つの値が似た値を取るときには、唯一すべての値の変動を考慮できる平均値だけを代表値として選択します。
身長や体重・テストの点数などで平均が計算されるのは、データの分布が比較的きれいな山型の分布であるためです。
きれいではない分布の場合
きれいではない分布の場合、代表値は中央値や最頻値を用います。
なぜなら、データの偏りや外れ値が存在するためです。
会社Bの年収の分布がきれいではない分布の1例になります。

平均値は約708万円、中央値や最頻値は約300万円と大きく値が異なっていますが、分布を見ると中央値や最頻値の方がデータの中央を捉えていますね。
このような場合には、中央値と最頻値を用いるのです。
有名な例として労働者の年収の分布は偏っていることが知られており、高所得者の年収に平均年収が影響を受けていることが知られています。
ですが、分布の山が2つあるような場合には、中央値や最頻値も使わないことをおすすめします。
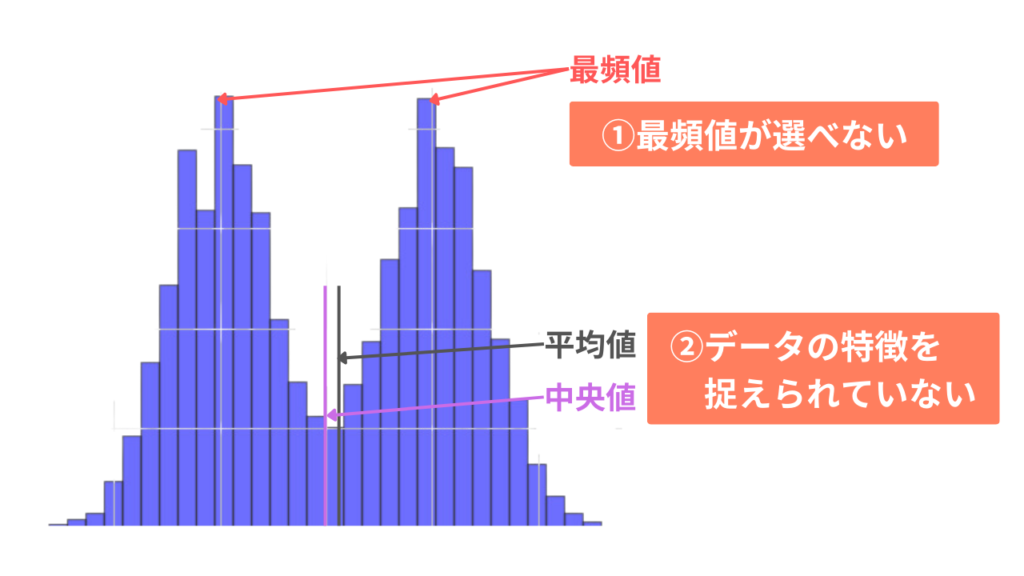
上図のようにデータの山が2つ存在していることから、最頻値は2つの山のどちらかを選べず、平均値や中央値がデータの特徴を捉えられていない状態になります。
そのため、このような場合では、山でデータを分けることできれいな山型の分布を2つ作り、それぞれのデータの分布を見るようにしましょう。
まとめ
データを使って代表値を出したい場合、なんでも平均でいいわけではありません。
データ分析を始める前に、データの特徴を掴んでデータ同士の比較を行うことなどに用いられます。
代表値には以下の3つの種類があります。
- 平均値
- 中央値
- 最頻値
代表値の選び方・使い分けは以下の2ステップで行います。
- ヒストグラムを作成する
- ヒストグラムの分布から代表値を選ぶ
代表値を選ぶためには、データの分布や極端な値(外れ値)がないかを確認する必要があります。
そこで、データの分布を見える化できるグラフであるヒストグラムを用います。
ヒストグラムから2つの場合の代表値の使い分けを判断できます。
- きれいな山型の分布
- きれいではない分布
きれいな山型の分布の場合、平均値や中央値、最頻値が近い値を取るため、すべての値を考慮できる平均値をデータの代表値として用います。
一方、きれいではない分布であった場合、平均値が極端な値(外れ値)の影響を受けている可能性が高いため、中央値と最頻値をデータの代表値として使用します。
また、山が2つあるデータの分布については、データを2つに分割することできれいな山型の分布を2つにして対応することがおすすめです。
もし自社で、「基本的な分析ができる人がいない…」「データをどのように扱っていいか分からない…」というお悩みがあれば、『かっこのデータサイエンス』にお問合せください。
状況のヒアリングを行い、お持ちのデータからデータ分析を行います。
サンプルデータの確認や課題の洗い出しまで無料で承っていますのでお気軽にご相談ください。(※データの集計や本データの分析、改善の実施には費用がかかります。)
詳細は以下のページからご確認ください。


























