「箱ひげ図ってどう見るのが正解?」と気になりませんか?
中高の数学で習った記憶があるものの、あまり使用する機会がないとどのような形のグラフか、そもそも何のために使われるグラフか忘れてしまいますよね。
箱ひげ図は、カンタンに作れるだけでなく比較も行えることからデータ分析の第1歩目として用いられます。
そこで本記事では、
- 箱ひげ図の見方
- 箱ひげ図の利点
について、初学者の方でも分かるように難しい用語や数式を使わずに説明していきます。
\経験豊富なかっこのデータサイエンティストがまとめました!/ 
箱ひげ図とは
箱ひげ図はデータを可視化するグラフの1つで、主にデータの分布を把握したい場合に使われます。
箱ひげ図を使うことのメリット・デメリットやエクセルでの作り方については以下の記事で解説しています。
下図のような箱ひげ図を用いて、箱ひげ図の見方について説明します。

上図のように、箱ひげ図は長方形の「箱」と「ひげ」と呼ばれる直線で構成されます。
箱ひげ図は、データを大きさ順に並べた時の分布を示しています。
値の軸が上向きなので、ひげの下側の末端が最小値、ひげの上側の末端が最大値を表しています。
最小値と最大値の間は、4つの区間に区切られていて、それぞれの区間が全体の25%のデータを収容しています。
それぞれの区間の切れ目は、
- 箱の下底:25%目のデータ
- 箱の中の横線:中央値(50%目のデータ)
- 箱の上底:75%目
のデータを表しています。
そのため、長方形(箱)の範囲にデータの真ん中50%が含まれています。
箱ひげ図では平均値を表現することもできます。上図では緑の三角形で示されている点が平均値です。
(中央値と平均値の違いについては『なんでも平均でいいの?』の記事を参照してください。)
上図のように、最小値から最大値の外部に点が表示されることがありますが、これらは外れ値と呼ばれます。
ここでは極端に大きい(小さい)ノイズのようなデータを外れ値と理解しておけば十分です。
箱ひげ図の見方と利点
次に、箱ひげ図の見方と利点について説明していきます。
ここでは、『データで判断! エンジニアの沖縄移住、おすすめエリア』で使用した家賃データを用いて、家賃50,000円以下の物件を探す際の、箱ひげ図の見方や利点について説明します。
まず、最寄り駅ごとの物件の平均家賃を示します。
以下の図から、どの駅の平均家賃も50,000円を超えていますが、その中でも経塚駅の平均家賃が最も50,000円に近いと分かります。
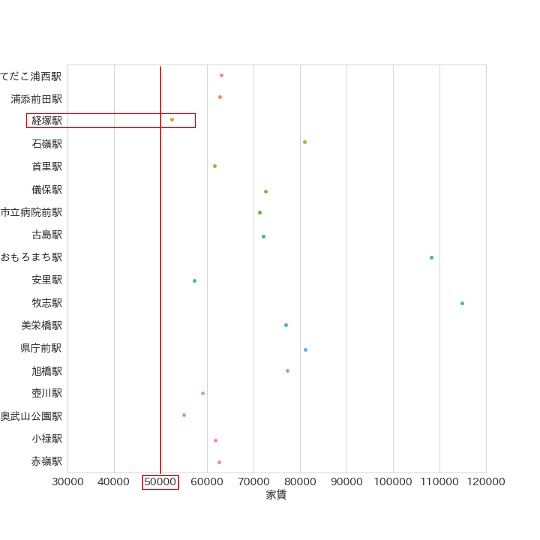
この情報から、家賃50,000円以下の物件を探す場合は、経塚駅が最も探しやすいと判断してしまいがちです。
しかし、平均値は極端に大きい(小さい)データの影響を大きく受けるため、平均値だけではどの価格帯の物件が多いかは分かりません。
例えば、経塚駅より家賃の平均値が高くなっている駅でも、少数の高級マンションの家賃の影響で平均値が高くなっている可能性があるのです。
そのため、家賃相場を読み取るためには、家賃の平均値だけでなく、分布も見る必要があり、データの分布を把握できるのが箱ひげ図なのです。
今回は、以下の図のように複数の箱ひげ図を用いて駅ごとの家賃の分布を見比べます。
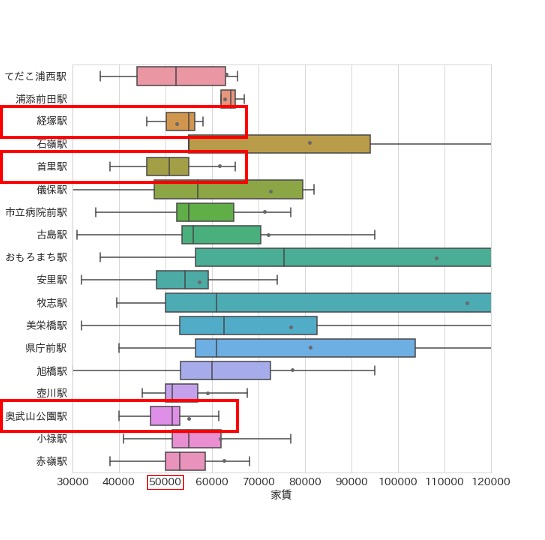
平均値は灰色の点で示してあります。
上図で家賃50,000円以下の部分に注目してください。
経塚駅では約25%の物件が家賃50,000円以下となっているのに比べて、首里駅、奥武山公園駅では約40%の物件が家賃50,000円以下となっています。
平均家賃は首里駅や奥武山公園駅より経塚駅の方が低くなっていましたが、首里駅や奥武山公園駅の方が家賃が低い物件の割合が高いと分かりますね。
なので、家賃50,000円以下の物件を探す際には、首里駅や奥武山公園駅が適していると判断できます。
このように、箱ひげ図を見ることで、平均値だけでは分からないデータの分布を把握することができます。
\経験豊富なかっこのデータサイエンティストがまとめました!/ 
本記事のまとめ
箱ひげ図の見方・利点について解説してきました。
箱ひげ図の利点は、
- 平均値だけでは読み取れないデータのばらつきを見れる
- データの分布を視覚的に把握できる
の2点です。
家賃分析では、平均値は低くなかったのに家賃は低いところが多い駅を見つけられました。
このように、データの全体像・分布を把握するのに用いられるのが箱ひげ図です。
また、箱ひげ図を使うことのメリット・デメリットやエクセルでの作り方については以下の記事で解説しています。
箱ひげ図でデータの全体像を把握した後、課題の解決をするために必要なアクションをみつけるデータ分析を行うのが、一般的です。
もし自社で、「データ分析をしたいけどできる人がいない…」「そもそもデータをどのように扱っていいか分からない…」というお悩みがあれば、『かっこのデータサイエンス』にお問合せください。
状況のヒアリングを行い、お持ちのデータから基礎的なデータ分析や課題解決のためのデータ分析を行います。
サンプルデータの確認や課題の洗い出しまで無料で承っていますのでお気軽にご相談ください。(※データの集計や本データの分析、改善の実施には費用がかかります。)
詳細は以下のページからご確認ください。