皆さんは「相関」という言葉を聞いたことがありますか??
「相関」はデータ解析に頻出する概念の1つであり、基本のキです。
しかし、統計やデータ解析に馴染みがない人にとって「相関」は、聞いたことはあるけどよくわからない、実はよくわかっていないものなのではないでしょうか。
そこで今回は、「相関」についてかっこ株式会社インターンをしている山科より説明したいと思います。
目次
相関とは2種類のデータの関連性を示す言葉
相関とは、2種類のデータの関係性を表している言葉です。
2種のデータに関係性がある場合、「その2種のデータには相関がある」
2種のデータに関係性がない場合、「その2種のデータには相関がない」
と言います。
では、「関係性」とはなんでしょうか。
関係性とは
片方のデータの値が大きくなった時の
もう片方のデータの値の変化状態
のことです。
例えば、
片方のデータの値が大きくなったときに、もう片方のデータの値も応じて大きくなると「その2種のデータには相関がある」
ことになります。一方、
片方のデータの値が大きくなったときに、もう片方のデータの値はその値に応じた変化ではなく、全く関係なく変化が起きていたり、特段大きくも小さくもなっていないと言った場合、「その2種のデータには相関がない」
ことになります。
正の相関と負の相関
2種類のデータに「相関がある」場合、その関係性は「正の相関」と「負の相関」の2つに分類されます。
正の相関は「一方のデータが大きくなればなるほど、もう一方のデータの値が大きくなる」という関係です。
負の相関は逆に「一方のデータが大きくなればなるほど、もう一方のデータの値は小さくなる」という関係となります。
2つのデータの関係性を把握するには、「散布図」と言う2つのデータの関係性をパッと見ただけで把握することができるグラフを用います。
散布図については、本サイト内で紹介記事を書いているのでぜひご覧ください。
(データの関係性がパッと見でわかる「散布図」)
この散布図をみると、横軸の値が大きくなればなるほど縦軸のデータも大きくなっています。このような関係を正の相関があるといいます。
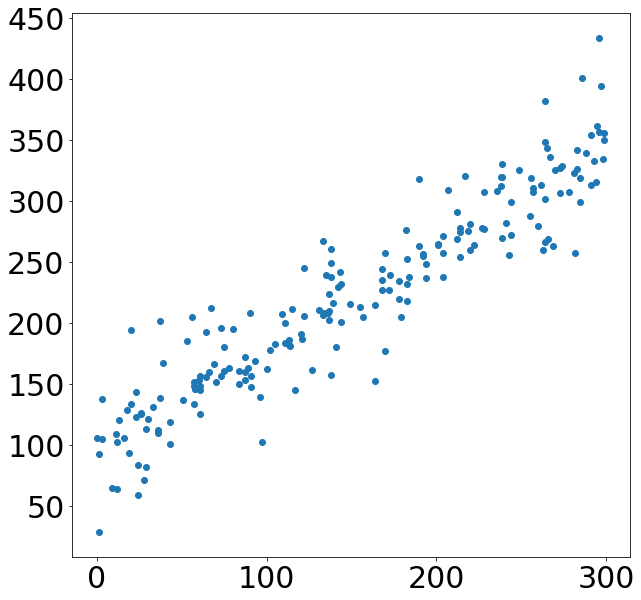
一方、こちらの散布図では、横軸の値が大きくなればなるほど縦軸のデータが小さくなっています。このような関係を負の相関があるといいます。
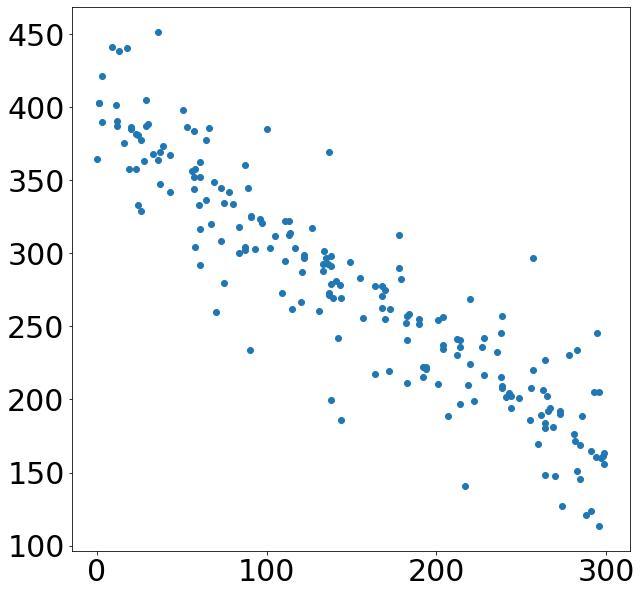
ちなみに、相関がない、無相関の散布図は例えば下図のようになります。横軸が大きくなっていても、それに応じる形で値の増減が起こっていないことが見て取れます。
相関の強さを数値で示す「相関係数」
相関は、「相関係数」を用いることで、その相関度合いがどの程度強いのかを数値で表すことができます。
詳細な計算過程は省きますが(「相関係数」で検索するとたくさんの解説ページがヒットします)、相関係数は-1~1の間で表され、1に近いほど正の相関が強く、-1に近いほど負の相関が強いと言えます。また、0に近いほど無相関であると言えます。
例で上げた正の散布図の相関係数は0.933、負の散布図の相関係数は-0.918
、無相関の散布図の相関係数は0.055です。
このように、相関がどの程度強いのかを見たいときは、相関係数を用いましょう。
相関活用法
ビジネスにおける「相関」の活用法といえば、「売上」や「利益」「コスト」といった経営の根幹となる数値や、顧客毎の購買・利用回数、売上金額といった重要指標に対し、別の種類のデータがどのように相関しているかを明確にすることで示唆を得ていくことなどがあげられます。
売上とは全く関係ないと思われていたデータに売上との相関があった場合、そこには売り上げを上げるヒントが隠されているかもしれません。
相関があって然るべきにも関わらず、相関係数が低いことがわかったら、なぜそのようなことが起きるのかを探っていくための第一歩となります。
例えば、売り上げが大きくなれば利益が大きくなることは当然の話です。つまり、売り上げと利益は正の相関があり、相関係数は1に近くなるはずです。それにもかかわらず、相関係数が0.2や0.3程度の低い相関しかないのであれば、そこにはなんらかの原因があるはずです。
もしその原因を把握していないのであれば、その原因を探ることは急務となるでしょう。
原因がわかれば、より売り上げや利益率を高めるための方策が見えてくるかもしれません。
相関に関する注意点
最後に、相関を扱う上での注意点についてお話しします。
因果関係とは違う
相関があるからといって、そこに因果関係があるとは限りません。相関は数値的に2種のデータの値の関連性を示すのみです。
「Aというデータの変化が原因となって、Bというデータが変化する」のかどうかまでは言えません。
疑似相関には注意せよ
疑似相関とは、2種のデータには全く関係性がないにもかかわららず、数値としては一見関係性があるために、その2種のデータが直接関係しあっているかのように見えてしまうことです。
本当に全く関係のない2種のデータが、値だけ関係しているという例もありますが、2種のデータに対し、”共通して相関があるデータ”が裏に潜んでいて、その2種のデータに相関が見られることもよくあります。
例えば、ある飲食店の暖かいスープの売り上げとスキー場の来訪者数に正の相関があったとします。
この場合、「どちらかのデータの変化と関連して一方のデータが変化している」とは言えないでしょう。
これは「気温が低い」ことで、両方のデータの値が増加すると考えるのが自然です。
散布図の結果が「直線的」でない場合、相関係数上は相関が無い。
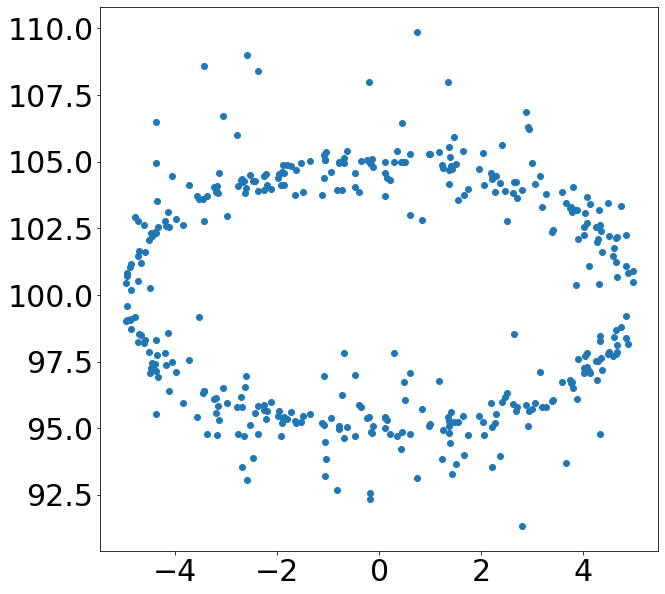
この散布図を見てください。
この2つのデータには、確実に何かしらの関係性があるように見えます。
しかしながら、片方が増えれば片方が増える・減るといったシンプルな関係性ではありません。
このような場合、相関係数としては「相関がある」と言えるような結果にはなりません。この散布図では相関係数は-0.013です。
散布図が直線的でない場合の関係性も示せるような指標はデータ解析界隈の論文で色々と提唱されているようですが、未だデファクトスタンダードはありません。
そのため相関を調べる際には、散布図と相関係数を同時にチェックすることが重要です。
相関係数は、2種のデータが共に定量データであるときに用いる
「定量データ」とは、測ることのできる客観的な数値データのことです。
金額や回数、距離、重さなどは測って比較することのできる数値といえますね。
一方、性別や居住地と言ったものは、測って比較することのできないものです。
他にも、アンケート調査でよくある「1.とてもそう思う 2.そう思う 3.どちらでもない 4.そう思わない 5.全く思わない」と言う値は一見数値データにも思えますが、数値の間に客観性はなく、定量データとは言えません。
こういったデータに対しては、基本的に相関係数は用いません。
こう言ったデータのでデータ間の関係性を見たい時は、クロス集計表や箱ひげ図、クラメールの連関係数やカイ二乗検定、相関比などなどを駆使して関係性を確認することがデータ解析分野では一般的です。
まとめ
- 相関とは、2種のデータの関係性を表している言葉で、「正の相関」「負の相関」「無相関」がある
- 相関を調べる時は、「散布図」&「相関係数」を使う
- 相関関係は因果関係ではない
- 疑似相関に気をつける
- 相関係数が低かったとしても散布図で関係性を確認する
- 相関係数の算出は定量データに限る
どんなデータがどの程度「売上」「コスト」「利益」と相関しているのかを解明することは、ビジネスにおけるデータ解析では極めて重要です。
かっこ株式会社では、実際にデータの整理、可視化、分析を行い、誰もがアクションに落とせる戦術作りを、お客様と一緒になって取り組んでいます。
データ分析に、はじめて取組むような企業様にも、安心して一歩を踏み出していただける「さきがけKPI」というサービスも、ご用意させていただいております。
ぜひご検討ください。