「度数分布表ってなに?」
「エクセルでも作れるの?」
と気になったことはありませんか。
度数分布表とは、データの特徴的なポイントを見つけるために用いられる表です。
また、度数分布表は代表値の計算やヒストグラムの作成などさまざまなことに活用できます。
ビジネスシーンでは、度数分布表から課題点を設定し、効果的なデータ分析につなげられます。
本記事では、
- 度数分布表に出てくる単語
- 度数分布表からわかること
についてわかりやすく解説していきます。
知識をおさらいして、データをよりうまく扱えるようにステップアップしていきましょう。
目次
度数分布表とは
度数分布表とはデータを自分で設定した範囲ごとに分割し、それぞれの範囲内に存在するデータを表にまとめたものです。
ただのデータを度数分布表にすることで、データの特徴や分布を把握でき、データ分析の手がかりを掴めます。
では、実際にただのデータから度数分布表にするまでの流れを解説していきます。
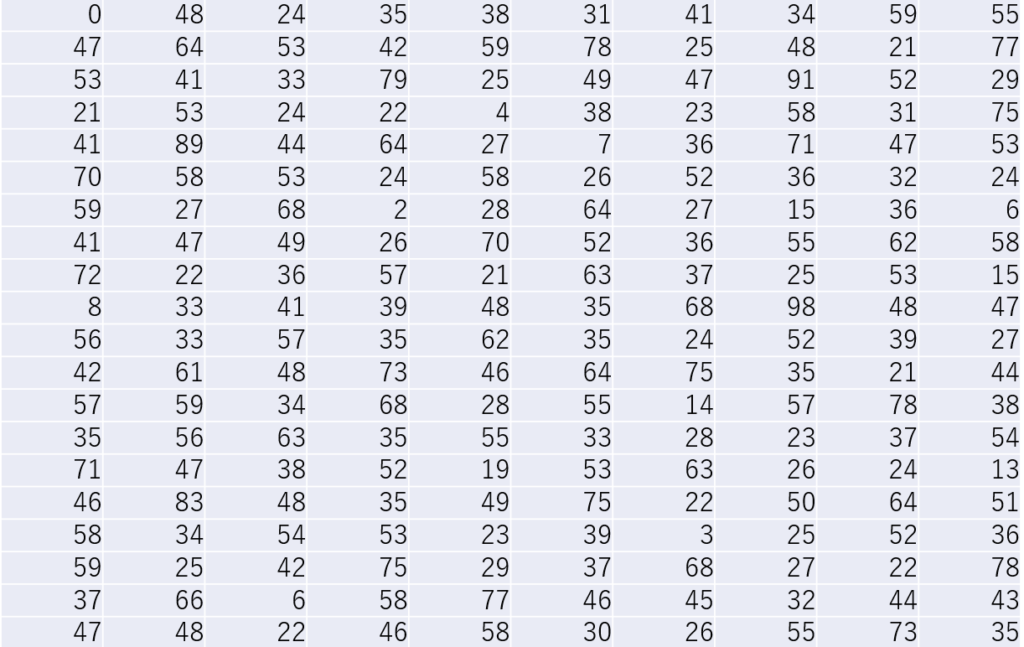
このように、今の状態だと単なるデータの羅列です。
このままでは、パッと見たときにデータの特徴を把握することはできません。
そこで、度数分布表にするためにこのデータを小さい順に並べ替え、データの範囲を指定して色分けしてみます。
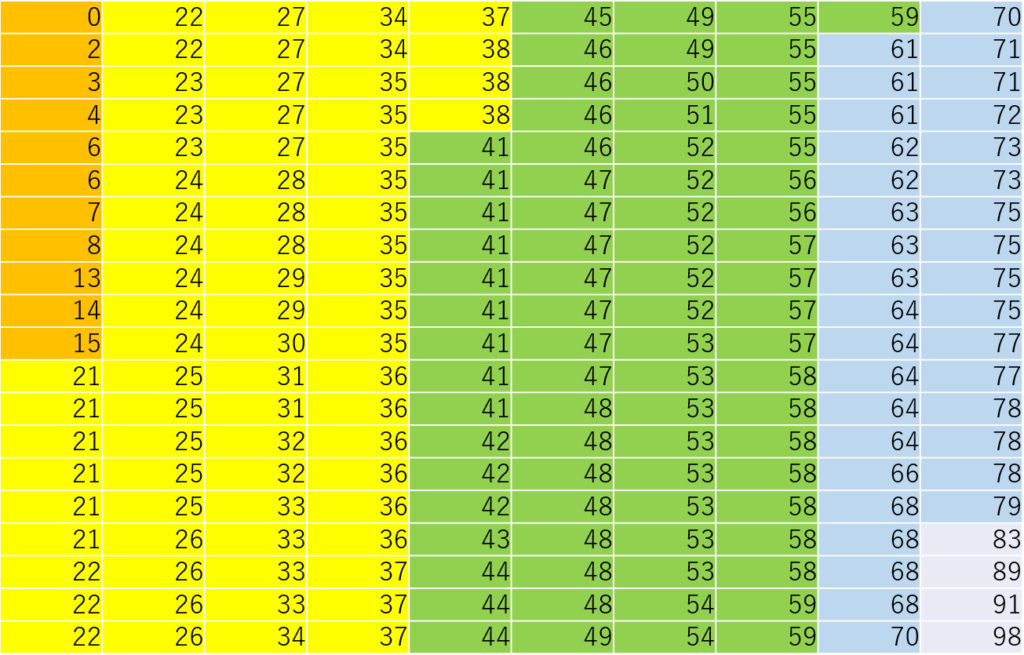
並び替えて色分けするだけとても見やすくなり、ただのデータの羅列から変化しました。
例えば、表の中で値が0~20のものは、図のオレンジ色の部分で11個のデータがある、というのが分かりやすくなっています。
そして、データの範囲でその個数を表にまとめていくと、下記のような表が完成します。
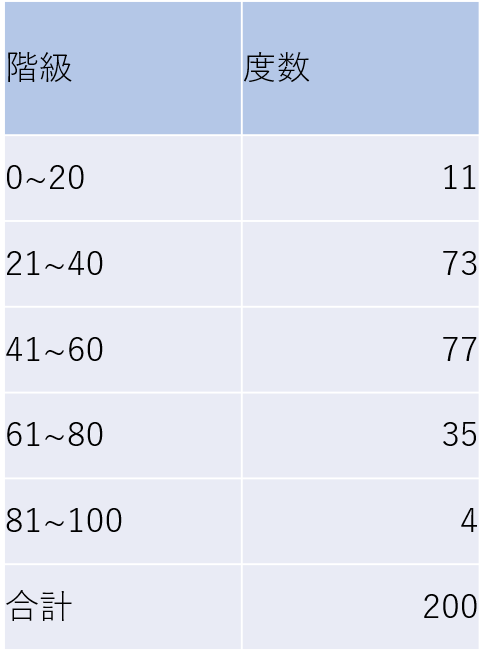
これを度数分布表と呼びます。
つまり度数分布表は、データを表にまとめる作業をするということです。
上図のままでも度数分布表と呼べるのですが、まだ分析に使えるような表にはなっていないため、さらに表を有効活用できるようにしたものが以下です。
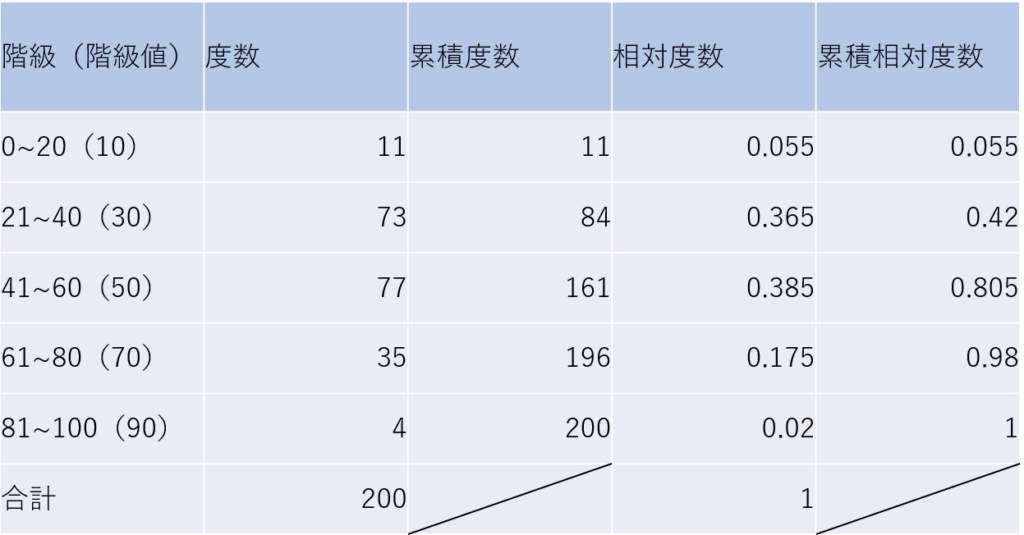
これが、冒頭の例のデータの度数分布表の完成版です。
ここまで整理できればデータ分析に有効に使えます。
度数分布表は6つの要素が必要
上の説明で分かるように、度数分布表は「階級」と「度数」などだけでも表として成り立ちます。
ですが、データ分析で有効活用できるようにするには6つの要素を出すべきです。
その6つの要素は以下のようなものになります。
- 階級:データを区切る範囲
- 階級値:階級の中央値
- 度数:区切られた範囲に存在するデータの個数
- 累積度数:その階級までのすべての度数の合計
- 相対度数:それぞれ階級の度数が全体に占める割合
- 累積相対度数:その階級までのすべての相対度数の合計
※単語の頭に累積とついているものは、それまでの階級の値をそれぞれ足していく数値です。
特に累積相対度数は、最終的に1になることが知られています。
これらの指標を確認することで、データの羅列だけでは掴みきれなかったデータの全体像や偏りを把握できて、業務効率化や売上向上などに使えるのです。
中央値について詳しく知りたい方は、『なんでも平均でいいの?』の記事をご参照ください。
それでは以下からは、この6つの要素の求め方をそれぞれ解説していきます。
度数分布表の6つの要素の求め方
階級、度数などの6つの要素はそれぞれ簡単に算出できます。
表にまとめると、以下のようになります。
| 要素 | 求め方 |
| 階級 | 区切るデータの範囲を自分で決定する |
| 階級値 | その階級の中央値を求める |
| 度数 | その階級内のデータの個数を求める |
| 累積度数 | その階級までの度数をすべて足し合わせて求める |
| 相対度数 | その階級の度数を全体のデータの個数で割って求める |
| 累積相対度数 | その階級までの相対度数をすべて足し合わせて求める |
階級を決定すると、中央値となる階級値とデータの個数である度数を求められます。
度数を計算できれば、累積度数と相対度数を算出していきます。
そして、相対度数から累積相対度数を算出して、度数分布表の完成です。
求める流れを図に表すと以下のようになります。
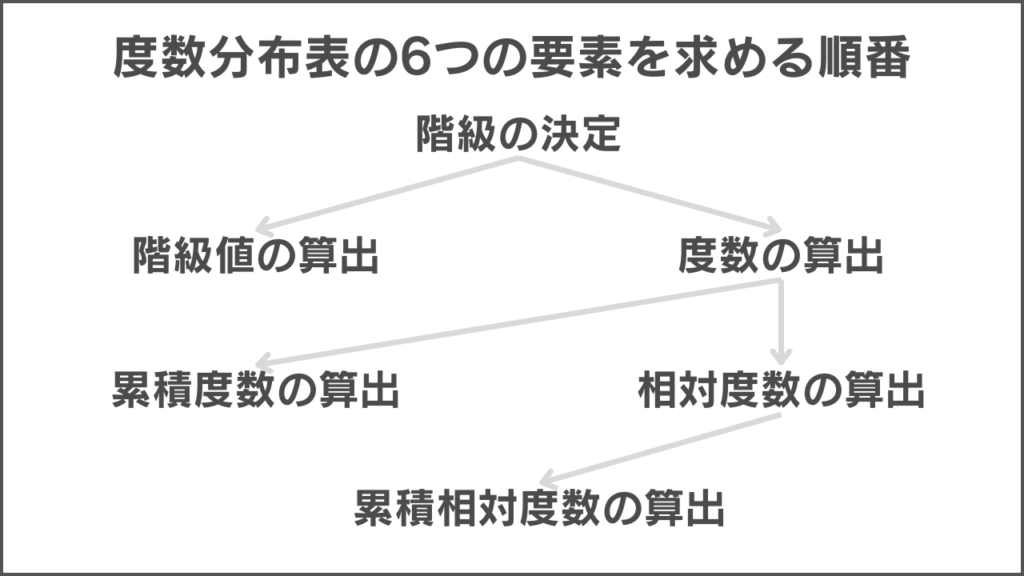
この順番を守ることで、より効率的に要素を求められます。
また、累積度数の最後の値はデータ数の合計、累積相対度数の最後の値は1になることを覚えておくと便利です。
度数分布表とヒストグラムの違い
度数分布表と同じように、データ分析に用いられるのが「ヒストグラム」になります。
ヒストグラムはデータをグラフ化させたもので、度数分布表とヒストグラムの違いは「表」か「グラフ」のどちらで示すか、です。

度数分布表とヒストグラムはどちらもデータの分布や特徴を把握するために利用されます。
しかし、度数分布表とヒストグラムは場合によって使い分ける必要があるので注意してください。
2つの違いについてまとめると以下のようになります。
| 表示形式 | 特徴 | |
| 度数分布表 | 表 | データの特徴を詳しく把握できる |
| ヒストグラム | グラフ | データの分布を視覚的に把握できる |
ヒストグラムは視覚的に把握できるようにするために、情報を絞って表示しています。
そのため、詳細なデータの特徴を掴みたいという場合は度数分布表に表す必要があります。
どこまで詳細に情報を知りたいかで度数分布表とヒストグラムを使い分けることをおすすめします。
もし、データの分布からどのようにデータ分析を進めればよいかに関心がある方は『ヒストグラムとは?見方やエクセルでの作り方・経営分析の例を解説』の記事をご参照ください。
ヒストグラムを適切に扱い、データを分析する方法を経営分析の例から解説しております。
それでは、実際に度数分布表を求めると何ができるのかについて解説していきます。
度数分布表を使ってできる3つのこと

度数分布表は、データを整理し特徴を理解できるようにする表です。
そのため、データ分析にする際の基礎分析に用いられます。
度数分布表を活用することで、できることは以下の3つです。
- データの特徴を示す値を求められる
- ヒストグラムが作成できる
- データから自社の課題点を見つけられる
度数分布表は度数などを把握できるだけでなく、他の値やグラフを作成するために活用できます。
それぞれ解説していきます。
①データの特徴を示す値を求められる
度数分布表を活用することで、データの特徴を表す値を求められます。
求められる値は主に以下の4つです。
- 平均値
- 中央値
- 最頻値
- 標準偏差
平均値や中央値、最頻値はデータの代表値と呼ばれ、データの特徴を代表する値です。
そのため、基礎分析ではこの3つの値が必ず求められます。
データの代表値とは何かについてまず知りたい方は『なんでも平均でいいの?』の記事をご参照ください。
また、標準偏差はデータのばらつきを表す値で、こちらもデータの散らばり具合を知るために用いられる重要な値です。
度数分布表を求めて活用することで、データの特徴がほとんど把握できます。
以下では、『度数分布表とは』の章で用いた度数分布表をもとに実際に計算していきます。

それでは、それぞれ解説していきます。
平均値を求める
度数分布表での平均値は、「階級値」と「度数」から計算します。
度数分布表での平均値は、それぞれの階級の階級値×度数の和をデータの個数で割ることで求まります。
例題で平均値を計算すると以下のようになります。
(10×11+30×73+50×77+70×35+90×4)÷200=44.8
度数分布表での計算は、その階級内のデータはすべて階級値とみなして計算します。
例えば、81~100の階級では、「83, 89, 91, 98」のデータがあります。
本来の平均値の計算だと、これらはすべて区別して足し合わせますが、度数分布表では以下のように階級内のすべての値を階級値の90であるとみなします。
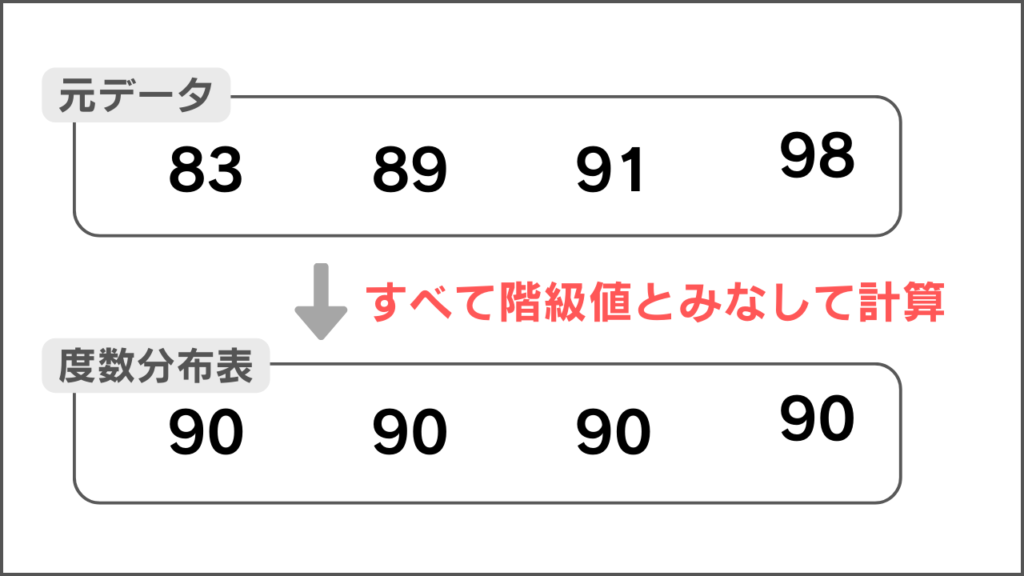
このように、階級内の値をすべて階級値であるとみなすため、本当の平均値とは違う値になってしまいます。
データ分析を進めていると、つい勘違いしやすいことであるため、必ず意識しておきましょう。
中央値を求める
度数分布表での中央値は、「累積相対度数」によって求められます。
どの階級にデータの中央があるのかを計算し、その階級値を中央値とします。
例題の表から、階級と階級値、累積相対度数のみを抽出して表示してみます。
| 階級(階級値) | 累積相対度数 |
| 1~20(10) | 0.055 |
| 21~40(30) | 0.42 |
| 41~60(50) | 0.805 |
| 61~80(70) | 0.98 |
| 81~100(90) | 1 |
累積相対度数とは、その階級までどのくらいのデータがあったかを示す値です。
累積相対度数を見ることで、累積相対度数が0.5を超えたところの階級にデータの中央値があると判断できます。
例のデータで中央値を確認してみましょう。

41~60の階級まででデータの50%以上があると判断できるため、41~60の階級値である50が中央値だとみなせるのです。
このように、累積相対度数をパッと見るだけで本当の中央値に近い値を見つけ出せます。
データの範囲(階級)を狭くすると、さらに中央値に近い値を求められることも覚えておくことをおすすめします。
最頻値を求める
最頻値は、「度数」もしくは「相対度数」から簡単に見つけ出せます。
度数分布表での最頻値は、どの階級に最も多くのデータが集まっているかの値です。
そのため、データ数である「度数」や全体に対するデータ数の割合を見れる「相対度数」を参照し、最も多い階級の階級値を最頻値とします。
| 階級(階級値) | 度数 | 相対度数 |
| 1~20(10) | 11 | 0.055 |
| 21~40(30) | 73 | 0.365 |
| 41~60(50) | 77 | 0.385 |
| 61~80(70) | 35 | 0.175 |
| 81~100(90) | 4 | 0.02 |
度数と相対度数のどちらを見ても、それぞれの階級は同じ大小関係であることが見て取れますね。
今回の例では、41~60の階級が度数と相対度数ともに一番大きい値であるため、最頻値は階級値である50と算出されます。
度数か相対度数のどちらかを参照することで、最頻値を求めるようにしましょう。
標準偏差を求める
標準偏差は「階級値」と「度数」、「平均値」から求められます。
まず、標準偏差について特徴や求め方をおさらいしておきたいという方は『標準偏差とは?データを見るなら知っておくべき求め方や目安』の記事をご参照ください。
それでは、標準偏差を求めていきます。
『平均値を求める』の章から、平均値は44.8だと判明しています。
平均値を基に、階級値から平均値を引き算し、偏差と偏差の2乗を求めます。
| 階級(階級値) | 偏差 | 偏差の2乗 |
| 1~20(10) | -34.8 | 1211.04 |
| 21~40(30) | -14.8 | 219.04 |
| 41~60(50) | 5.2 | 27.04 |
| 61~80(70) | 25.2 | 635.04 |
| 81~100(90) | 45.2 | 2043.04 |
偏差を2乗するのは、誤差を足し算する時にお互いの値で打ち消しあわないように値をすべてプラスにするためです。
偏差の2乗をそれぞれの度数で掛けます。
| 階級(階級値) | 度数 | 偏差の2乗 | 度数×偏差の2乗 |
| 1~20(10) | 11 | 1211.04 | 13321.44 |
| 21~40(30) | 73 | 219.04 | 15989.92 |
| 41~60(50) | 77 | 27.04 | 2082.08 |
| 61~80(70) | 35 | 635.04 | 22226.4 |
| 81~100(90) | 4 | 2043.04 | 8172.16 |
度数×偏差の2乗の和を求めると61972となり、データ数で割ると分散、平方根を取ると標準偏差です。
今回の例では、標準偏差が約17.6と算出できました。
このように、度数分布表を用いることで、データの代表値や標準偏差といった特徴的な値を算出できるのです。
②ヒストグラムが作成できる
度数分布表からヒストグラムを作成できます。
度数分布表にはヒストグラムの作成の際に必要なものが揃っています。
それぞれの対応関係は以下のようになります。
- データの範囲:階級
- データの個数:度数
このように、度数分布表があればヒストグラムを作成できるため、基礎的なデータ分析では度数分布表が作成されます。
③データから自社の課題点を見つけられる
ビジネスでは、度数分布表は課題点を見つけることに用いられます。
度数分布表を見ることで、どのデータの範囲にデータが集まっているのか、集まっていないのかなど特徴を把握できます。
例えば、データを分析しようとなったとき、何から分析したらいいか分からない…となったことはありませんか。
度数分布表を用いることで、課題点を明確に見つけ出せるのです。
『かっこのデータサイエンス』では、サンプルデータの確認や課題の洗い出しまで無料で承っています。
お気軽にご相談ください。(※データの集計や本データの分析、改善の実施には費用がかかります。)
【簡単】度数分布表をエクセルで作る方法
度数分布表はエクセルで簡単に作れます。
エクセルで操作できるため、自社のデータをそのまま関数で処理して、度数分布表を作成可能です。
今回は、以下のようなステップで度数分布表を作成していきます。
- 階級幅を決める
- FREQUENCY関数を用いて度数を計算、そして累積度数を計算する
- 相対度数・累積相対度数を求める
また、補足として度数分布表からヒストグラムを作成する方法についても解説していきます。
今回は0~100までのデータを100個ランダムで生成したデータから度数分布表を作成します。
乱数は以下の関数で作成しています。
=RANDBETWEEN(0,100)
それでは度数分布表を作成していきましょう。
STEP1. 階級幅を決める
まず、階級は自分で決めなくてはなりません。
5ずつにするのか、10ずつにするのかで結果は大きく変わります。
エクセルでの例では20ごとの範囲で階級を設定します。
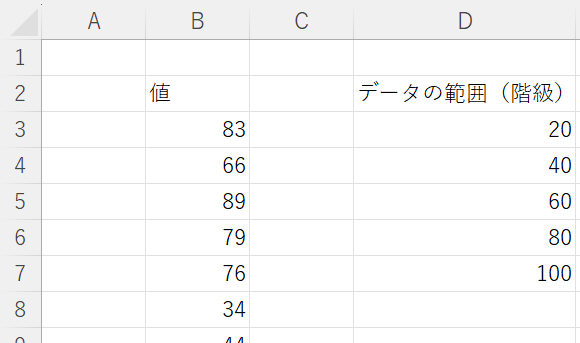
0~20のように記述していないのは、次のステップでの計算方法が関係しています。
それでは次のステップです。
STEP2. FREQUENCY関数を用いて度数を計算、そして累積度数を計算する
度数の計算にはデータと区間を指定すると、度数を自動で算出してくれるFREQUENCY関数を使用します。
FREQUENCY(データ配列,区間配列)とそれぞれ設定する値が設けられています。
今回の例では、データ配列にはすべてのデータ、区間配列では最後の100だけ除いて範囲指定します。
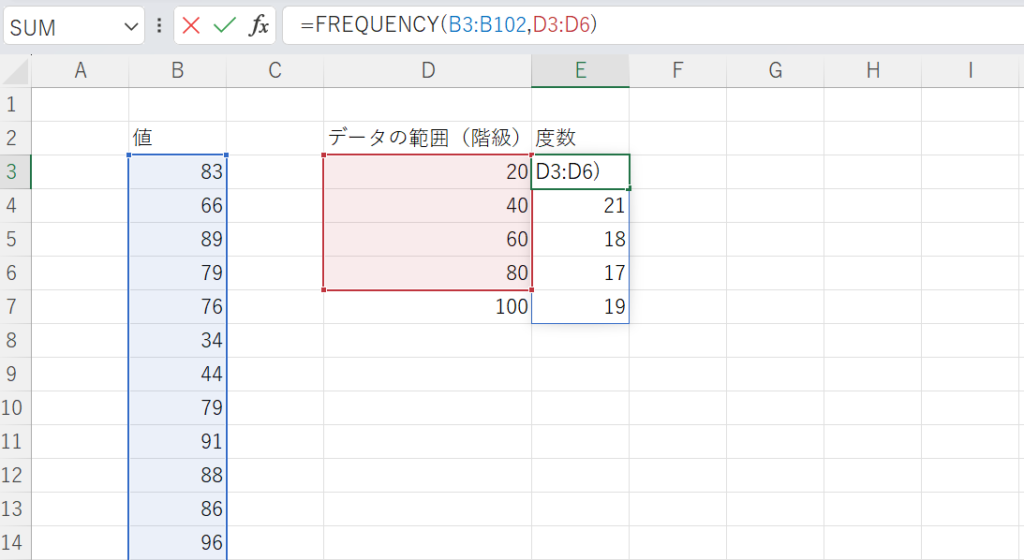
上記のように、
=FREQUENCY(B3:B102,D3:D6)
と入力することで、度数を自動で計算してくれます。
この時、区間の指定は一番下を除くことを忘れないでください。
そ度数が求まれば、SUM関数で足し算を行い、累積度数を求めます。
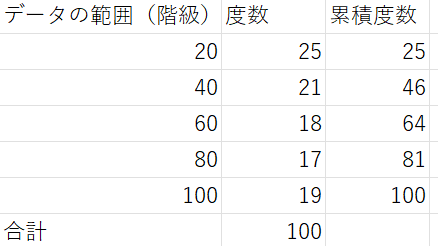
ここまで完成すれば、最後のステップに移ります。
STEP3. 相対度数・累積相対度数を求める
相対度数は階級の度数÷合計データ数で求めます。
今回の例では、度数や合データ数はE列に格納しているため、
=E3/$E$8
のように入力すると、0~20の階級の相対度数が求まります。
相対度数が求められれば、累積度数と同じ要領で累積相対度数を計算します。
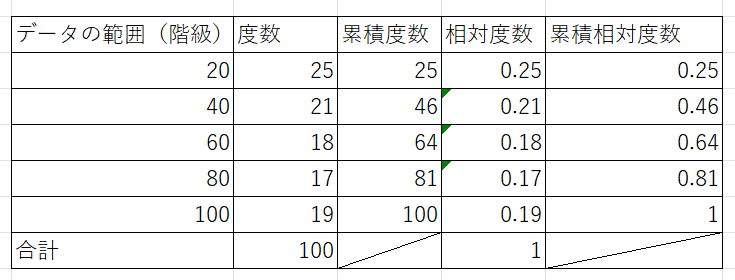
枠線等を装飾すると、以下のような度数分布表が完成です。
ここまで完成すれば、
- 度数の合計はデータ数と一致しているか
- 累積度数の最後はデータ数と一致しているか
- 相対度数の合計は1か
- 累積度数の最後は1か
の4つを確認することをおすすめします。
全て確認できれば、度数分布表の作成は終了です。
以下では、補足としてヒストグラムの作成方法を解説します。
【補足】度数分布表からヒストグラムを作成する
ヒストグラムの作成には、度数分布表の「階級」と「度数」を用います。
度数分布表とヒストグラムの要素を照らし合わせると以下のようになります。
- それぞれの棒(ビン)のデータの範囲:階級
- データの範囲内のデータの個数:度数
上記の対応関係をヒストグラムの作成の際には頭に入れておくことをおすすめします。
度数分布表の階級と度数の列を合計以外すべてドラッグし、挿入タブ>おすすめグラフ とクリックすると、棒グラフのようなものが表示されます。
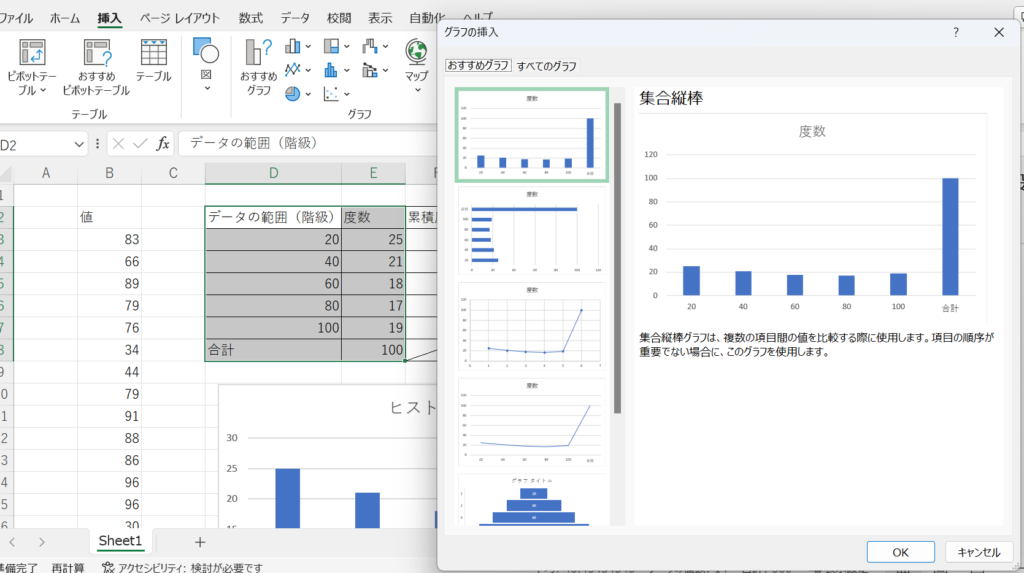
度数分布表からヒストグラムを作成する場合は、棒グラフを作成します。
直接ヒストグラムを選択しても、正しいヒストグラムにならないので、注意してください。
おすすめグラフから集合縦棒を選択し、タイトルを変更すると以下のようなヒストグラムが完成します。
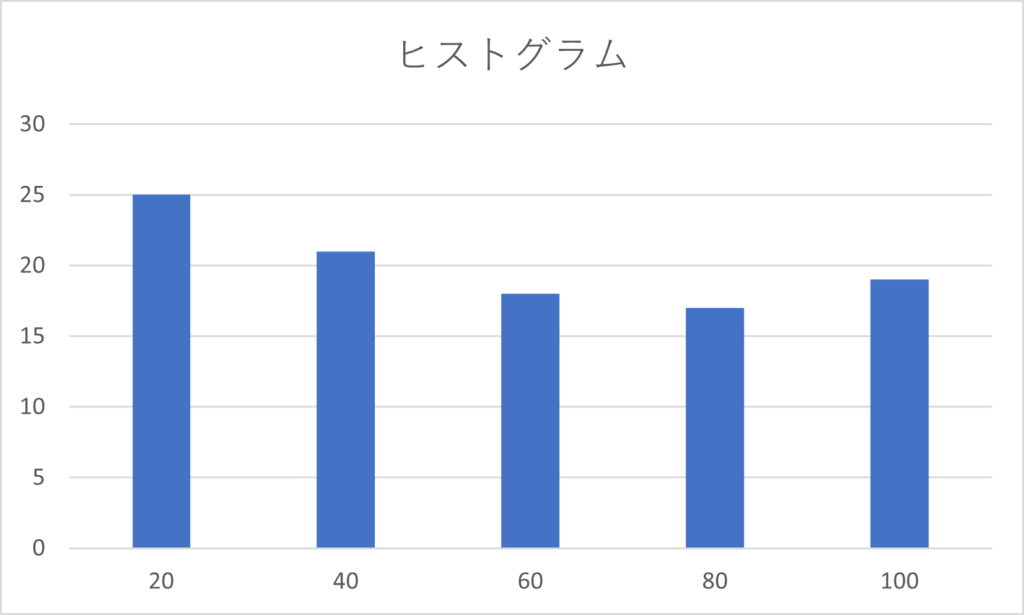
もし、元データがある場合は、元データを選択し、ヒストグラムのボタンからヒストグラムを作成する方が簡単です。
ヒストグラムを元データから作成する方法は『ヒストグラムとは?見方やエクセルでの作り方・経営分析の例を解説』の記事をご参照ください。
度数分布表からわかることを例を用いて解説
度数分布表を活用することで、データの特徴を詳しく把握できます。
この章では、実際にどのように度数分布表を活用して、分析につなげられるかを解説していきます。
下記の表は2020年に厚生労働省により発表された『2019年 国民生活基礎調査の概況』に記載のある、【各種世帯別にみた所得金額階級別世帯数の分布及び中央値】に関する度数分布表です。
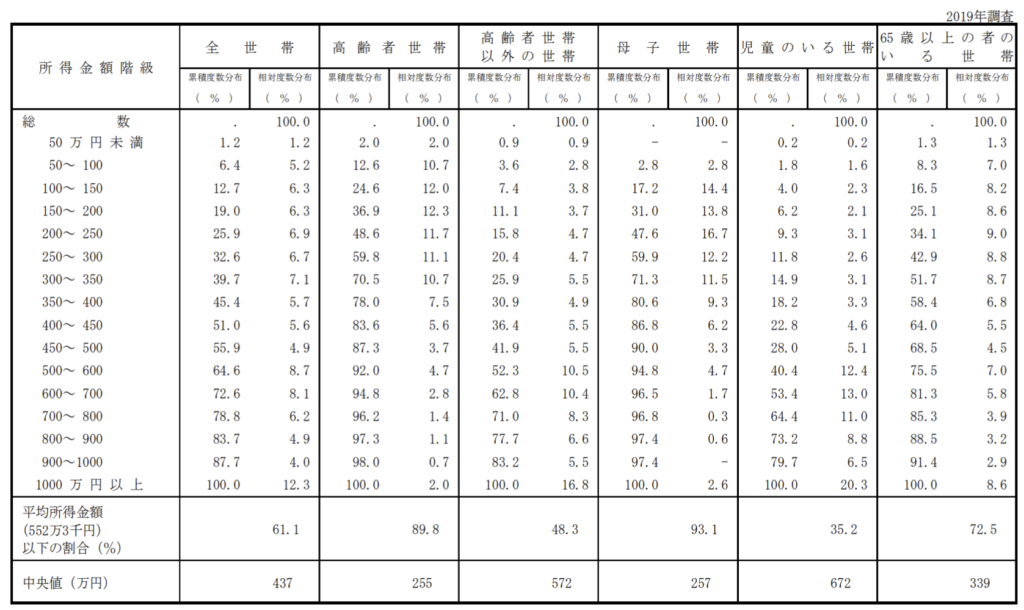
少し見づらいので、全世帯に絞って表示してみます。
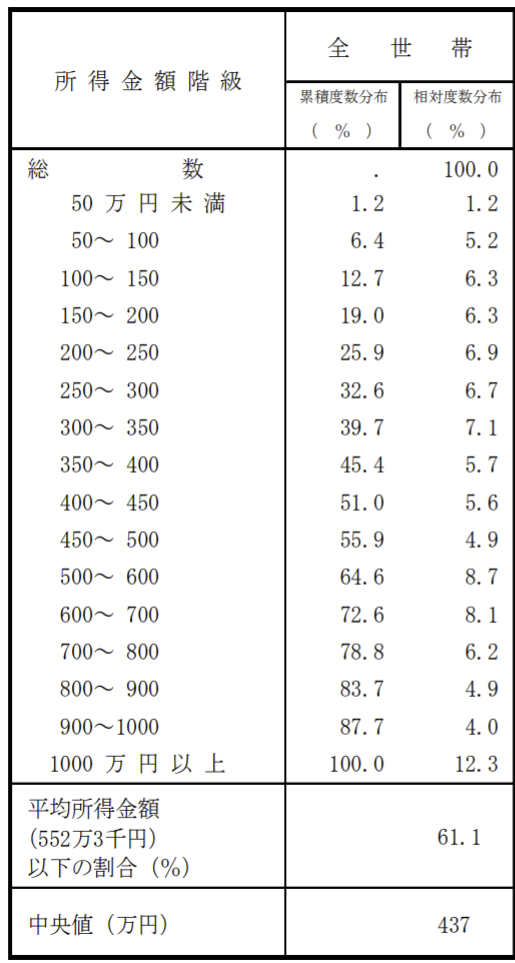
上の章で取り上げた表とはレイアウトが少し異なっていることが読み取れます。
「度数」の表示がなく、「累積度数」と「相対度数」のみがパーセント表示で表されていますが、度数分布表としての機能は保たれています。
この度数分布表の以下の部分に注目してみましょう。
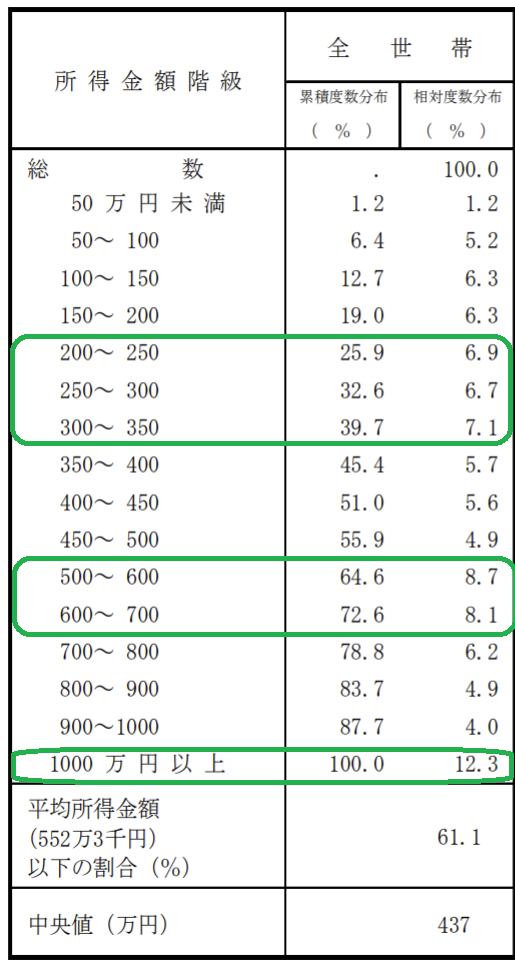
緑で囲われた部分を見てみると、他の階級に比べ相対度数(分布)の値が大きいため、3つの階級に属する世帯が他の階級より多いとわかります。
度数分布表の相対度数を用いることで、ある範囲内に存在するデータが全体のデータのどの程度を占めており、どの階級が多いのかを一目で理解できます。
度数分布表を見ることで、データ中にある偏りや散らばりといった特徴を掴めるのです。
まとめ
度数分布表とはデータを決められた範囲ごとに分割し集計したものです。
度数分布表を見ることで、データの偏りや散らばりといった特徴を掴めます。
度数分布表を解釈するためには以下の単語を押さえておく必要があります。
- 階級
- 階級値
- 度数
- 累積度数
- 相対度数
- 累積相対度数
それぞれの要素の計算は以下のような表で覚えておくことをおすすめします。
| 要素 | 求め方 |
| 階級 | 区切るデータの範囲を自分で決定する |
| 階級値 | その階級の中央値を求める |
| 度数 | その階級内のデータの個数を求める |
| 累積度数 | その階級までの度数をすべて足し合わせて求める |
| 相対度数 | その階級の度数を全体のデータの個数で割って求める |
| 累積相対度数 | その階級までの相対度数をすべて足し合わせて求める |
また、度数分布表とヒストグラムの違いも正しく認識しておきましょう。
| 表示形式 | 特徴 | |
| 度数分布表 | 表 | データの特徴を詳しく把握できる |
| ヒストグラム | グラフ | データの分布を視覚的に把握できる |
度数分布表からヒストグラムにしてしまうと、累積度数などの情報が削られてしまいます。
そのため、詳細な情報を知りたい場合は度数分布表を用いることをおすすめします。
度数分布表は簡単な表でありながら、以下のことに活用できます。
- データの特徴を示す値を求められる
- ヒストグラムが作成できる
- データから自社の課題点を見つけられる
度数分布表からデータの代表値や標準偏差を算出できます。
しかし、階級内の値をすべて階級値と扱う点に注意しておきましょう。
度数分布表は以下のステップを踏むことで、エクセルで簡単に作成できます。
- 階級幅を決める
- FREQUENCY関数を用いて度数を計算、そして累積度数を計算する
- 相対度数・累積相対度数を求める
また、「階級」と「度数」を用いて棒グラフを作成することで、ヒストグラムも作成可能です。
日本における全世帯の所得に関するデータの分析の例からも分かるように、度数分布表を用いることでデータの特徴を詳しく把握できます。
もし自社で、「データ分析をしたいけどできる人がいない…」「そもそもデータをどのように扱っていいか分からない…」というお悩みがあれば、『かっこのデータサイエンス』にお問合せください。
状況のヒアリングを行い、お持ちのデータから基礎的なデータ分析や課題解決のためのデータ分析を行います。
サンプルデータの確認や課題の洗い出しまで無料で承っていますのでお気軽にご相談ください。(※データの集計や本データの分析、改善の実施には費用がかかります。)
詳細は以下のページからご確認ください。































