みなさんオッズ比ってご存じでしょうか?
売上や利益をあげるために、有益なアクションが100個あったとしても、そのすべてが結果に同じ影響力を持っているわけではありません。
そのうちの5個しかやる時間が無いとしたら、どれがいちばん、効果的なの?
を明らかにしてくれる方法論、それが「オッズ比」です。
今回はそんなオッズ比についてわかりやすく紹介していきます。
オッズ比について
オッズ比の意味とは、ある事象の起こりやすさを2つの群で比較して示す統計的な尺度のことをいいます。
そして、オッズとは、ある事象の起こる確率と起こらない確率の比のことです。
オッズ比は、言葉通り2つのオッズの比になります。
式はそれぞれ次の通りのイメージです。
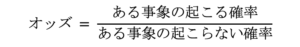
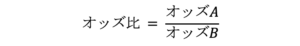
では具体的な例でその使い方を見ていきましょう。
販促のキャンペーンを実施した際の結果で下記のようなデータがあるとします。

まず準備としてこのデータをもとに次のような表を作成します(これをクロス集計表といいます)。

※作成するときは左側に原因、上側に結果としてください
では実際にオッズ比を算出してみましょう。
左側については、キャンペーン対象6名とキャンペーン非対象3名の比で、「2」の購入オッズが得られます。一方で右側について、キャンペーン対象6名とキャンペーン非対象12名の比で、「0.5」の非購入オッズが得られます。
そして、この2つのオッズの比2/0.2をとり、オッズ比4が算出されます。
このようにして1つのクロス集計のデータから2つのオッズと1つのオッズ比が得られます。
そしてこのオッズ比の数値の見方ですが、1を基準として1から離れているほど結果に対して原因が強く影響しているというように判断します。
つまり今回の結果は、キャンペーンによって購入が促されているらしい、ということが言えます。
※よく誤解しがちなのですが、キャンペーンをやった方がやってないより4倍購買するというのは間違った解釈です。
参考までにオッズ比が1になる(つまり結果と原因に強い関連性がない)のはこのようなクロス集計表が得られる場合です。

このデータでみると直感的にキャンペーンによって購買を促せてなさそう、というイメージがつくのではないでしょうか。
ここまでは、オッズ比の算出と得られる判断材料について簡単な例で説明してきました。
でも、これだけだと、明確な基準のあるカイ二乗検定でも、同じ目的が果たせます。
では、なぜ、オッズ比を使うのか、どうしてオッズ比が便利なのか、次でお話ししていきます。
オッズ比の有効活用法とは
以前、ご紹介した「カイ二乗検定」は、原因と結果が関連していそうかという質問に対して、はい/いいえを確かめたいとき使われます。
もしも複数の原因が関連していそうだ、という結果が得られたとき、その中で、どれがより強く関連しているのか、知りたくありませんか?
このような比較をしたいシーンで活躍するのがオッズ比です。
以下の例では、カイ二乗検定によって2つのビジネスに有意義な結果が得られています(キャンペーンA、Bによって購入が促されている)。ここでどちらが人数的に効果があったのか比較をしようとするならばどう判断しますか?

2つの結果についてそれぞれオッズ比を算出してみましょう。
キャンペーンA:購入ありオッズ(100/100)/購入なしオッズ(200/1000)=5
キャンペーンB:購入ありオッズ(150/150)/購入なしオッズ(300/1200)=4
オッズ比の見方は、1から離れているほど強く結果に影響しているということでした。
つまり、キャンペーンAの方が購入されやすいという結果が得られます。
このほかにも、例えば、顧客分析において優良顧客と不良顧客の特徴の違いを可視化するために様々な顧客情報を比較してみたり、商品分析において特にどんな商品を売り出していくべきか、に関して有意義な判断材料が得られます。
このようにオッズ比の魅力は、統計的な検定によって目的を達成するための要因が複数明らかになったとき、どの要因がより、ビジネスにインパクトを与えるのか、定量的に比較して、アクションするうえでの優先順位を付けられることにあります。
経験や仮説・勘に基づいて意思決定をすると、どうしてもシチュエーションによって判断の信頼性に対する疑念が生じたり、検証のための時間もたくさん、かかってしまいます。
カイ二乗検定やオッズ比には、客観的統一的な視点で、かつ定量的に比較ができる、というメリットがあります。
有効なアクションを見つけるだけでなく、それを用いて高速にPDCAを回したいような時、強力なツールとなるのです。
まとめ
オッズ比は、
目的達成に貢献する要因に、優先順位をつけてくれる
さぁ、あなたの抱えるビジネス課題でも、オッズ比にもとづいて、効率よく成果をあげてみたくなりましたよね?
かっこの定額分析サービス「さきがけKPI」では、オッズ比を使った、目的達成のお手伝いも低価格でご提供できます。
ぜひ、ご相談ください。









