経営判断や、次のアクションを決める必要があるときに、「どんな要素が」「どの程度」影響を与えているのかや、投資に対するリターンの期待値を事前に知ることができたら心強いと思いませんか?
- 新規店舗をオープンするにあたり、売上高に影響する要因と、それが、どの程度の影響をあたえるのか
- 投下した広告宣伝費に対して、どの程度の売上(リターン)が期待できるのか
- 来週一週間で商品Aが何個くらい売れそうか
蓄積されたデータをもとに、過去の実績からこのような問に答えてくれるのが「回帰分析」です。
本記事では、「回帰分析」について紹介したいと思います。
なお、本記事では ”変数”、”量的変数”、”質的変数” といった専門用語を使用しています。
これらついては、こちらの記事で説明していますので、よければこちらの記事を御覧いただいてからお読みください。
(データ分析の成果を大きく左右する「変数」って何だ?)
回帰分析とは?
「回帰分析」とは、蓄積されたデータをもとに、複数の変数間の関係を
y = ax + b
といった式に落とし込む統計手法です。
例えば、このような過去の月間の広告宣伝費と売上の関係を示す架空のデータがあるとします。
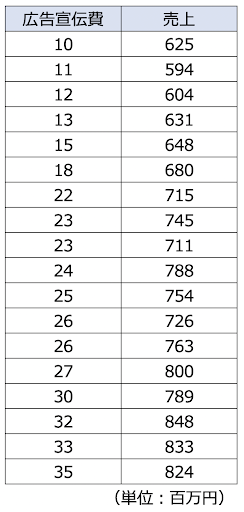
このデータを、散布図で表現してみます。
(散布図については、こちらの記事で解説していますのでよければご覧ください
データの関係性がパッと見でわかる「散布図」)
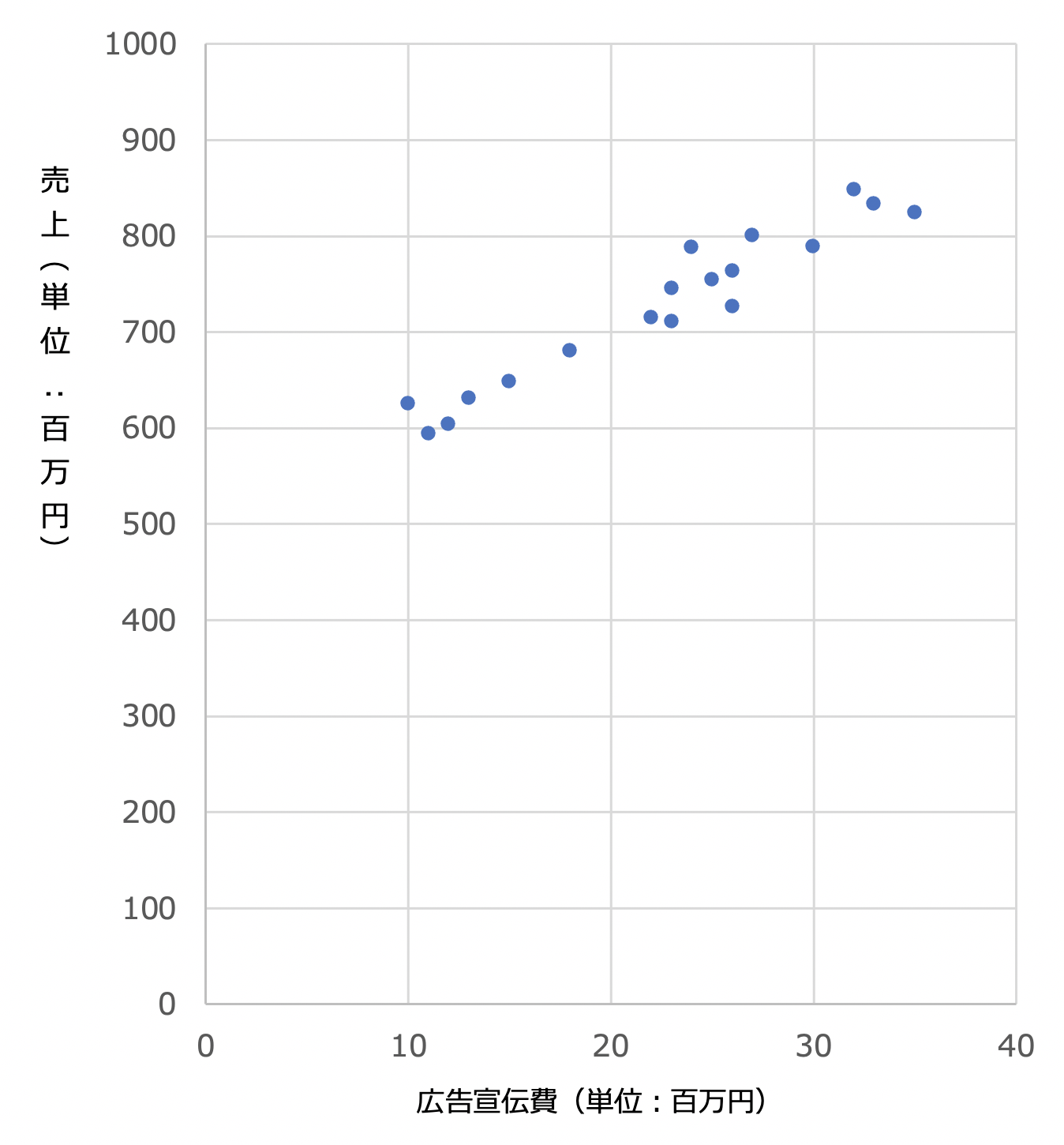
ここで、相関を見てみましょう。
(相関については、こちらの記事で解説していますので、よければ御覧ください。
2種のデータの関係性を明らかにする「相関」のおはなし)
広告宣伝費をかけるほど売上が上がるという関係性が読み取れ、相関係数は0.965であるため、非常に高い正の相関があります。
散布図と相関によって、広告宣伝費をかけるほど売上が上がるという関係性が明らかになりました。しかし、これだけでは、かけた投資に対してどの程度のリターンが返ってくるかがわかりません。
そこで登場するのが回帰分析です。
「回帰分析」とは、蓄積されたデータをもとに、複数の変数間の関係を y = ax + b の式に落とし込む統計手法だと前述しました。この広告宣伝費と売上データを用いて、回帰分析を行うと、このような結果になります。
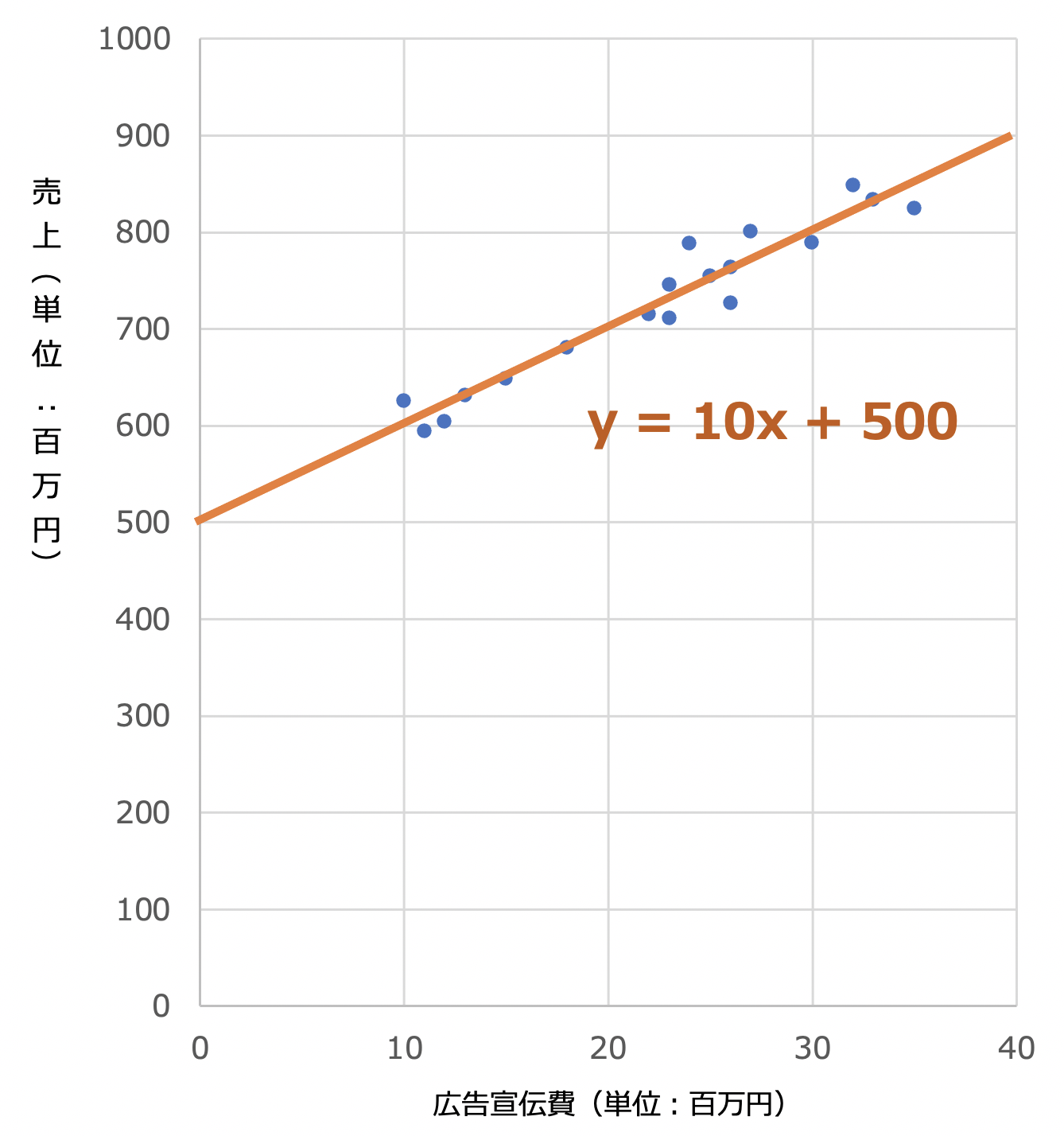
回帰分析を行うことで、
y(縦軸、売上) = 10x(横軸、広告宣伝費) + 500
という式ができました。
この式から、「100万円広告宣伝費を増やすと、1000万円売上が増える」という、広告宣伝費と売上の関係性がわかりました。
なお、 回帰分析では 左辺の y にあたる変数を「目的変数」や「従属変数」、右辺のxにあたる変数を「説明変数」や「独立変数」と呼びます。
今回の回帰分析では売上が目的変数(従属変数)、広告宣伝費が説明変数(独立変数)ということですね。
以上のように、目的変数と説明変数の関係を方程式の形で表現する統計手法、それが回帰分析です。そして、回帰分析の結果、得られた式を回帰式と呼びます。
実は、ExcelやGoogleスプレッドシートでも回帰分析の計算をすることができます。
本ブログでもGoogleスプレッドシートでの計算手順については、こちらの記事で紹介していますので、よければ御覧ください。
(実は簡単! 10分あれば回帰分析ができます)
回帰分析の種類
回帰分析には様々な種類があります。
前項で紹介したのは、目的変数が量的変数で、説明変数が1つのみの『単回帰分析』という一番シンプルな回帰分析手法です。
説明変数が複数の回帰分析は『重回帰分析』と呼ばれています。
例えば、都内繁華街にチェーン展開をしている飲食店で、実店舗の実績データをもとに「売上」を目的変数とし、「駅からの距離」「終電時間」「駅の乗降車数」「席数」などの複数の変数を説明変数として、式に落とし込む手法が重回帰分析です。
説明変数と目的変数が同じ変数で、過去の結果が未来の結果にどのように関係するかを回帰式にする手法もあります。
例えば、「過去の商品売上個数」を説明変数にして、「将来の商品売上個数」を目的変数とする回帰式で、これを「自己回帰モデル」などと呼びます。
目的変数が「買った」「買わなかった」のような2つの値のみの質的変数の場合は、確率を計算する『ロジスティック回帰』という手法が使われます。
(ロジスティック回帰については、こちらの記事で紹介していますので、よければ御覧ください。
確率を予測する「ロジスティック回帰」とは)
また、目的変数が3つ以上の値の質的変数のときは、回帰分析の『多項選択モデル』という手法が使われることが多いです。
他にも、目的変数自体の偏りやばらつき、目的変数と説明変数の関係性やそれに伴う計算過程、そもそものデータ分析の目的などによって、様々な手法が扱われます。
が、とにかく押さえておくべき点としては、回帰分析とは、蓄積されたデータを元にして、目的変数と説明変数の関係を式に落とし込む手法であり、いろいろな事象をより的確な回帰式として表現するための様々な手法が存在している、ということでしょう。
回帰分析の使いどころと注意点
ビジネスシーンにおいて、回帰分析を行うことで得られる目的変数と説明変数の関係性を表現した回帰式の活用方法は主に下記の3つでしょう。
重要な指標に影響を与える要因と、その影響度合いの把握
前述の都内繁華街にチェーン展開をしている飲食店の例がこれに当たります。
「売上」を目的変数とし、「駅からの距離」「終電時間」「駅の乗降車数」「席数」などの複数の変数を説明変数とした重回帰分析を行って回帰式を得ることで、どの説明変数が、どの程度目的変数である売上に影響を与えているかを把握することができます。
このように、重要な指標に対して、どのような変数が影響を与えているのか、また、その影響度合いはどの程度なのか、を客観的な数値で把握する、というのが回帰分析の使い所の1つです。
投資に対する期待値の把握とコントロール
先程例に示した、広告宣伝費と売上の回帰式の活用がこれにあたります。
得られた回帰式より、100万円広告宣伝費をかけるごとに1000万円の売上が増えるという関係性がわかりました。
この関係性の把握により、広告宣伝費にいくら投じたら、いくら売上が上がり得るかという期待値が把握できます。
一方、原材料調達不足による在庫減少時などに、機会損失を起こさないために抑えたい売上高に対してどの程度の広告費をかけるべきか、といったときの広告宣伝費のコントロールに用いることも可能となります。
将来予測
「過去の商品売上個数」を説明変数にして、「将来の商品売上個数」を目的変数とする回帰式を用いて将来の売上個数を予測する、といったことも可能です。
将来の売上個数の予測ができれば、機会損失を減らしつつ、かつ、在庫もできる限り持たないような運用を行っていくことが可能となるでしょう。
もちろん、前項までに例示した、飲食店の売上に関する回帰式や、広告宣伝費に対する売上に関する回帰式でも、それぞれの説明変数に値を代入することで、目的変数の値について予測をすることが可能です。
注意点
このように回帰分析は、ビジネスにおいて経営から現場までが判断材料として活用できる非常に便利な手法です。
ただし、得られた回帰式は、あくまでも過去の実績データから得られた結果だ、ということを忘れてはなりません。
言わずもがなですが、経営を取り巻く環境や社会は刻一刻と変化し、ずっと同じ状況が続くということはありえません。
回帰分析の目的次第ではあるものの、基本的に過去の実績データから得られた回帰式は、社会情勢が変わった後にはそのままではほぼ活用できないものと考えたほうが良いでしょう。
例えばコロナ前のデータを用いて作成した、首都圏の飲食店の売上予測を行うための回帰式が、withコロナ時に活用できるものにはならない、というのは想像に難くありません。
そのため、回帰分析実施にあたり、あまりに古いデータを用いるのはNGでしょうし、一度回帰式を作成した後も、常に時代に沿ったものとするために回帰式のアップデート(計算・検討のし直し)を定期的に行うといった姿勢が必要でしょう。
最後に、こういった注意しなければならない点はあるものの、ビジネスにおける判断を行う際、客観的な数値として測れる結果を判断材料とすることができるため、回帰分析は非常に使いでのある手法であることを再度付け加えておきます。
まとめ
- 回帰分析とは、蓄積された実績データをもとに、目的変数と説明変数の関係を方程式の形で表現する統計手法である。回帰分析の結果、得られた式を回帰式と呼ぶ。
- ビジネスにおいて、回帰分析は下記のようなシーンで大きな武器になる
- 重要な指標に影響を与える要因と、その影響度合いの把握
- 投資に対する期待値の把握とコントロール
- 将来予測
- 得られた回帰式はあくまで過去の実績データから得られた結果である。
ビジネスの判断材料として活用するには、刻々と変わる社会情勢に対応するためにも、常にアップデートする姿勢が大事である。
かっこのデータサイエンスでは、本記事で紹介している回帰分析をはじめとし、貴社の課題に合わせて柔軟に手法を選択しながらデータ分析を用いた課題解決を実施いたします。
是非お気軽にご相談ください。








