「回帰分析ってなに?」
「回帰分析はどんなところで活用されてる?」
「回帰分析はどうやってやるの?」
と気になりませんか。
回帰分析とは、調べたいデータの項目(変数)の間の関係性を数式にして、現状の傾向の把握や予測を行う統計学の分析手法です。
回帰分析を行えるようになることで、データの特徴や傾向を把握し、現状の傾向の把握をもとに未来の予測や意思決定に役立てられます。
本記事では、
- 回帰分析の種類
- 回帰分析の活用事例
- 回帰分析の手順
などについて解説していきますので、ぜひ参考にしてください。
\経験豊富なかっこのデータサイエンティストがまとめました!/ 
目次
回帰分析とは

回帰分析とは、調べたいデータの項目(変数)の間の関係性を数式で表現することで、現状の把握を行ったりある変数から他の変数の値を予測したりする統計学の分析手法です。
現状の把握と将来の予測のどちらにも利用できることから、多くのデータ分析でも用いられている分析手法です。
代表的なものとして、回帰分析には3つの種類があります。
- 単回帰分析
- 重回帰分析
- ロジスティック回帰分析
3つの種類の違いを簡単にでも把握しておくことで、回帰分析の理解度が一気に変わってきます。
なので、まずはそれぞれの回帰分析について詳しく解説していきます。
種類1. 単回帰分析
単回帰分析は1つの変数ともう1つの変数の関係を分析する最も基本的な回帰分析になります。
回帰分析の基礎となるのが単回帰分析であり、重回帰分析は単回帰分析の応用版とも言えるので、必ず単回帰分析を理解しておきましょう。
例えば、以下のような2つの項目の組み合わせの分析を行う場合に単回帰分析が用いられます。
- 売上と広告費の関係
- アイスクリームの売上と気温
- 試験の成績と学習時間
以上は一部の例であり、他にも日常の様々なところで単回帰分析が用いられているのです。
分かりやすい分析例として、チェーン店を展開するパン屋が新しい店舗を開くときの売上予測を行ってみます。
今回は架空のデータで、それぞれの店舗の「平均売上」と「駅の平均利用者数」から単回帰分析を行います。
まずは、2つの変数の関係を散布図で用いて表しましょう。

散布図についておさらいしておきたい方は『データの関係性がパッと見でわかる「散布図」』の記事をご参照ください。
単回帰分析では、上図のように散布図を用いることでパン屋の売上と駅の利用人数の関係性をざっと把握することが重要です。
そして、予測を行うための式(回帰式)を算出します。
実際に、予測を行う式(回帰式)から直線(回帰直線)を散布図上に描いてみると以下のようになります。
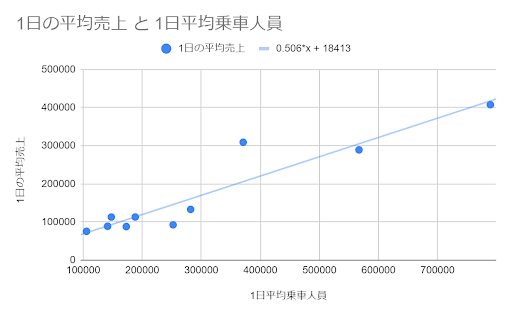
上図のように、回帰式から直線(回帰直線)を描いて関係性を把握できるようにするのが単回帰分析です。
そして、今回の例の場合だと、以下のような回帰式が求められます。
\[ 1日の平均売上 = 0.506 \times x(1日平均乗車人員) + 18413 \]
このように、単回帰分析では、回帰式で2つの変数の関係性を表すことで現状の把握を行えます。
また、xに「1日平均乗車人員」の値を入れることで、以下のように「1日の平均売上」の予測もできるのです。
\[ 1日の平均売上 = 0.506 \times 50000 + 18413 = 43713 \]
回帰分析は、現状の傾向の把握だけでなく、予測も行える点で、便利な分析手法なのです。
ですが、回帰分析では関係性までしか分からないため、駅の利用人数が多いからパン屋を出店したら儲かる、というような因果関係までは言い切れない点に注意しておきましょう。
種類2. 重回帰分析
重回帰分析は、予測したい項目に対して、2つ以上の項目との関係性を分析した場合に用いられる分析手法です。
単回帰分析は予測したい変数に対して1つの変数だけでしたが、重回帰分析では2つ以上の変数から関係性を分析できます。
以下のように、複数の要因との関係性を把握したい場合に、重回帰分析が用いられます。
- 家賃における部屋の広さ、立地、築年数の影響
- 健康状態における運動量、食事、睡眠時間の影響
- 売上における気温、最寄り駅の利用人数、イベントの有無
以上のように様々な要因が考えられる場合は、単回帰分析でなく重回帰分析を用います。
例えば、単回帰分析で行った「パン屋の売上予測」でも、駅の利用人数だけじゃなくて季節性やイベントによる影響も含めたい場合に、重回帰分析が用いられます。
このように複数の要因を考えたい場合に、複数の要因の関係性を分析できるのが重回帰分析なのです。
種類3. ロジスティック回帰分析
ロジスティック回帰分析は、予測したい項目が「はい・いいえ」で答えられる項目である場合に用いられる回帰分析になります。
単回帰分析や重回帰分析は予測したい項目が数値である必要があるため、「はい・いいえ」で答えられる項目を予測する場合にはロジスティック回帰分析が用いられるのです。
例えば、以下のような項目を予測したい時に用いられます。
- 病気が発症するかしないか
- 商品を購入するかしないか
- 試験に合格するか合格しないか
ロジスティック回帰分析は、以上のような場合で確率を予測したい場合に適しています。
もし、予測したい項目が数値でない場合には、ロジスティック回帰分析を用いることを検討しましょう。
「ロジスティック回帰分析をもっと詳しく知りたい」という方は『ロジスティック回帰分析とは?使える場面や実装まで徹底解説』の記事をご参照ください。
回帰分析でできる2つのこと

回帰分析の3つの種類でも触れていますが、回帰分析は大きく2つのことを行えます。
回帰分析を利用することでできることは以下の2つです。
- 現状の傾向を把握できる
- 現状の傾向から未来の予測ができる
それでは、それぞれ詳しく解説していきます。
現状の傾向を把握できる
回帰分析を用いることで、データの様々な傾向やパターンを明らかにでき、データの特徴を把握できます。
データ分析を行う時にまず行うのがデータの特徴を把握することであり、データの特徴の把握で回帰分析が用いられることがあるのです。
例えば、以下のような状況の分析でデータの把握に回帰分析が用いられます。
- 商品の売上状況の分析
- 不動産価格の分析
- 人口状況の分析
回帰分析を行うことで売り上げや価格などの項目に対して、関係性を見たい項目との関係性を数値で表せます。
また、その関係性がどのくらい強いのかまでを把握できることから、様々な分析でデータの把握に用いられているのです。
現状の傾向から未来の予測ができる
回帰分析を行うと、現在のデータから回帰式を立てられるため、項目間の関係性の傾向から未来を予測できます。
回帰分析では過去のデータに基づいて回帰式を作っているため、関係性を表した回帰式を用いることで、近い未来の傾向を推定できます。
例えば、以下のような未来の傾向の予測を行えるでしょう。
- 商品の売上推移
- 株価の予測
- 人口の推移
データサイエンスの技術を使った予測の方が精度が高くなることが多いため、回帰分析はデータの特徴を把握する場面で主に使われているのです。
なので、以下からは回帰分析を使った現状の傾向の把握に特化して、解説していきます。
\経験豊富なかっこのデータサイエンティストがまとめました!/ 
回帰分析を使った現状の傾向の把握はこんなところで使える!

回帰分析はデータの傾向やパターンを明らかにでき、便利であることから、様々な分野で用いられています。
この章では、以下の3つの例に絞って解説していきます。
- 現状の売上状況の把握
- 現在の需要の傾向の把握
- 不動産価格の決定
それでは、それぞれ詳しく解説していきます。
現在の売上状況の把握
回帰分析は、売上の現状を知るためにも使えます。
店舗を持っている・サービスを持っているなど、事業を起こしていれば、あなたの事業の売上の現状を知ることはとても重要です。
また、この回帰分析を使うことで、現状の改善すべきところも知れるため回帰分析が使えると事業運営が効率化できます。
例えば、売上との関係性を見る項目として、以下のようなものが考えられます。
- 製品の価格
- 広告やキャンペーン
- 経済状況 etc.
以上の項目以外にも様々な項目から回帰分析を行うことで、どの要因がどのくらい売上と関係があるのか・ないのかを確認できます。
例えば、価格が売上と関係しているのであれば、最適な価格をもう一度考え直すことで、売上を改善できる可能性があるのです。
とはいえ、業界によって考えるべきことも大きく異なるため、適切な回帰分析を行うにも技術が必要になります。
現在の需要の傾向の把握
事業を起こしている場合、需要の傾向を把握することも重要であり、回帰分析によって現在の傾向を把握できます。
回帰分析を使うことで、需要に関係している項目を見つけられるため、需要に合った在庫管理や生産計画をある程度考えられるのです。
需要に関係している可能性がある項目として、以下のようなものが挙げられます。
- 人口動態
- 経済状況
- 季節性 etc.
以上のような項目との関係性を見ることで、現在の需要を把握でき、在庫管理や生産計画を最適化できます。
しかし、「需要予測」となると回帰分析ではなく、データサイエンスの技術を使った方が精度が上げやすいです。
なので、あくまで需要との関係性の把握をするために回帰分析を用いることをおすすめします。
「需要予測について詳しく知りたい!」という方は、『需要予測とは?使える場面や予測の手法・注意点を徹底解説!』の記事をご参照ください。

不動産価格の決定
回帰分析を用いることで、不動産価格の決定のために必要な情報も把握できます。
不動産の価格を決定するには多くの情報が必要で、その一つに家賃の相場も挙げられますが、相場を把握するためにも回帰分析を利用できます。
不動産価格に関係している項目として、以下のようなものが考えられます。
- 立地
- 坪数
- 築年数 etc.
以上のような項目で回帰分析を行うことで、どの項目がどのように不動産価格と関係しているのかを知れます。
不動産価格の回帰式を求められるため、ある不動産の情報からおおよその価格を算出できて、不動産価格の決定の参考になるのです。
10分でできる回帰分析の手順

回帰分析で現状の傾向を理解するためには、3つの手順が重要です。
手順通りに進めることで、回帰分析を用いて効率的に現状の傾向の把握を行えます。
3つの手順は以下の通りです。
- 【STEP1】現状を把握したい項目とその関係性を見たい項目を選ぶ
- 【STEP2】回帰分析を行う
- 【STEP3】回帰分析の結果を解釈する
それぞれの手順について、詳しく解説していきます。
【STEP1】現状を把握したい項目とその関係性を見たい項目を選ぶ
現状を把握したい項目と関係性を見たい項目を選ぶことから始めます。
どの項目を選ぶかによって分析の質が大きく変わるため、適当に選ばないようにしましょう。
関係性を見たい項目を選ぶ時は、以下のような項目がないか確認することをおすすめします。
- 現状を把握したい項目と関係してそうな項目
- 関係しているかは分からないが関係性を調べたい項目
- 一見、関係性がなさそうな項目
注意しなければならないのが、関係性のありそうなものだけを選んではいけないということです。
関係性がなさそうな項目であっても、「関係性がない」と判断するために回帰分析に入れてみましょう。
もし入れるかどうか迷うようであれば、とりあえず選んでみて結果を見てみることをおすすめします。
【STEP2】回帰分析を行う
回帰分析に用いる項目が選べたら、回帰分析を行います。
回帰分析を行うにしても、いきなり回帰分析を行ってはいけません。
回帰分析を行う前に、以下のことを行いましょう。
- データの前処理:欠けている値の処理やスケーリング(単位を揃える)など
- モデルの選択:線形回帰、ロジスティック回帰など、目的に応じた回帰分析モデルを選択
回帰分析を正しく行うには、項目のデータを回帰分析に適した形に調整しなければなりません。
また、どの回帰分析手法を用いるかも重要ですので、どの回帰分析を行うのかをはっきりさせておきましょう。
準備が整えば、エクセルやPythonなどで回帰分析を行うことをおすすめします。
【STEP3】回帰分析の結果を解釈する
回帰分析を行ったら、正しく結果を解釈する必要があります。
なぜなら、回帰分析の解釈を正しく行えなければ、現状を把握したい項目との関係性を説明できないためです。
結果の解釈には、以下のような指標を用います。
- 回帰係数:各項目と現状を把握したい項目との相関の大きさ
- 決定係数:モデルの推定値がどれだけ良く当てはまっているか
- p値:各項目が統計的に有意か(どれだけ意味がありそうか) etc.
以上のような指標から、回帰分析の結果をしっかりと解釈することで、初めて回帰分析を行うことに価値が生まれます。
なので、回帰分析を用いた現状の傾向の把握は、結果の解釈まで行う必要があることを忘れないでください。
回帰分析を簡単に行う4つの方法【ツール・プログラミング】

回帰分析を簡単に行う方法は多くありますが、今回は4つの方法を紹介します。
この記事で紹介する方法は以下の4つです。
- エクセル
- Googleスプレッドシート
- R
- Python
以上の4つの方法を以下のデータの例を用いて説明していきます。

上図は単回帰分析の説明で用いたデータの回帰分析を表したグラフになります。
以下の表が実際のデータです。
| 1日平均乗車人員 | 1日の平均売上 |
| 789366 | 407557 |
| 370856 | 309041 |
| 566994 | 289068 |
| 281971 | 133063 |
| 188170 | 113090 |
| 147699 | 112910 |
| 252267 | 92577 |
| 141351 | 88798 |
| 173003 | 87856 |
| 105669 | 75573 |
回帰分析を行うためのそれぞれの方法について手を動かしながら確認してください。
それでは、それぞれ詳しく解説していきます。
エクセルでの回帰分析
エクセルは多くの方が利用しているツールであり、回帰分析も簡単に行えます。
なぜなら、エクセルでは既に回帰分析を行うためのツールが用意されているからです。
エクセルで回帰分析を行う場合、以下のような手順で行います。
- データ分析のアドインを追加する
- 「データ」タブの「データ分析」ツールを開く
- 「回帰」オプションを選択し、分析するデータ範囲を指定する
- 出力範囲を設定し、結果を得る
まず、Excelを開いて、ファイル>その他>オプションをクリックします。
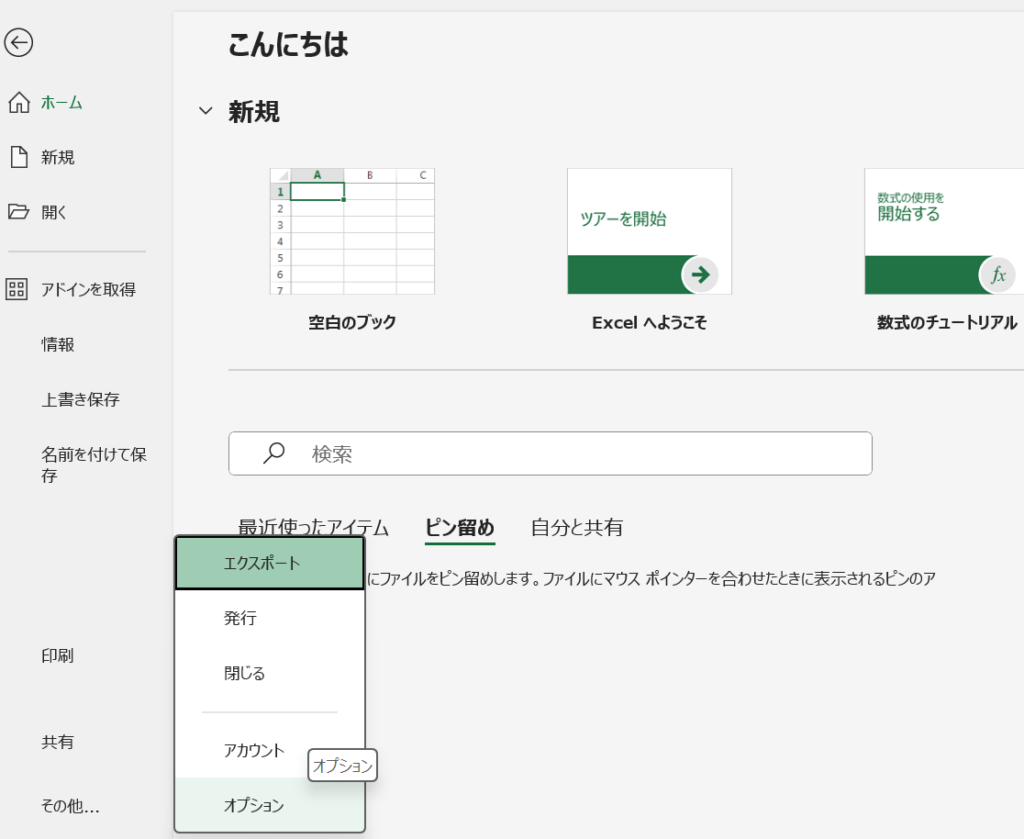
すると、以下のような画面になるので、アドイン>下の方にある設定をクリックしてください。
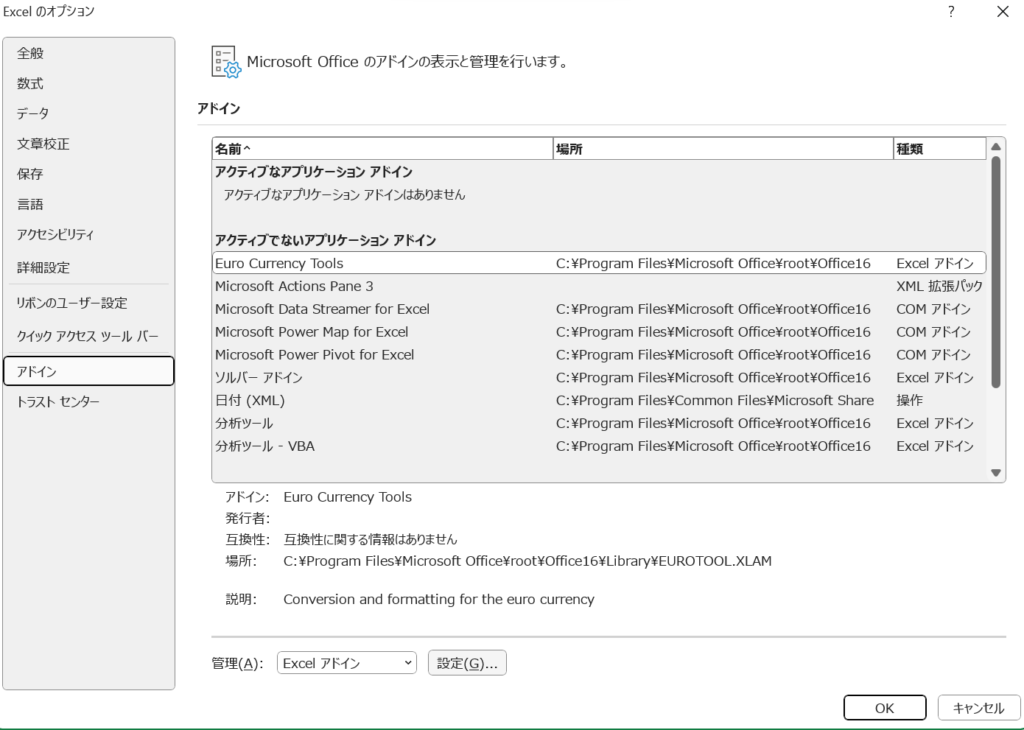
設定を押すと以下のような画面になるので、分析ツールをチェックしてOKを押します。
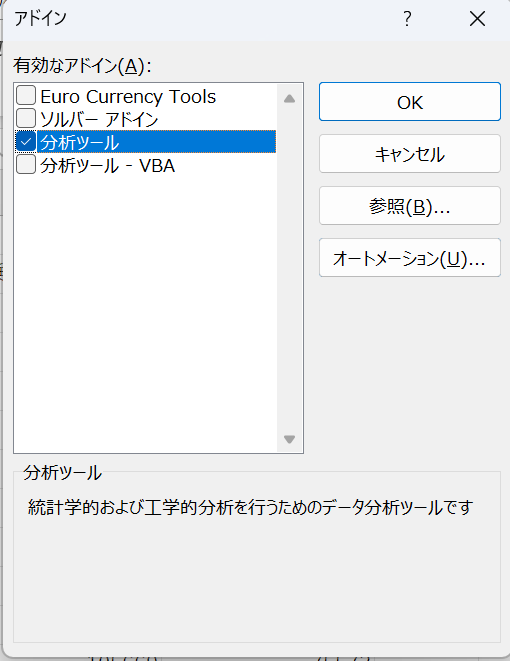
エクセルに戻って、データタブをクリックしてもらうと、右側に「データ分析」ができていると思います。

表のデータをエクセルにコピーしてから、データ分析ボタンを押すと以下のような画面が出てきます。
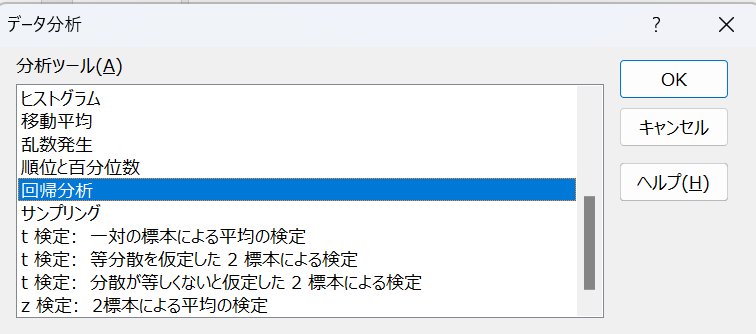
回帰分析を選択して、OKを押してください。
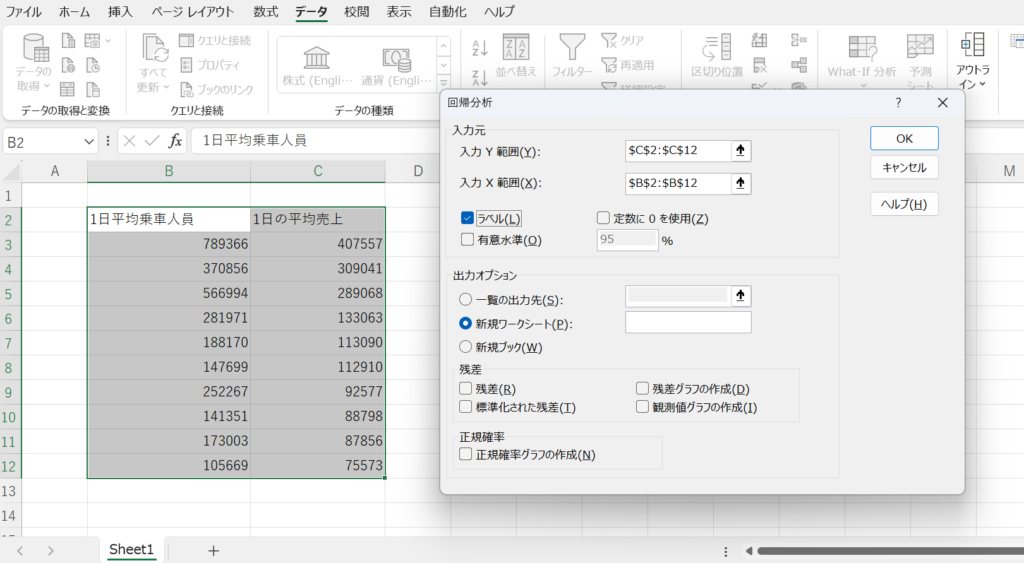
上図のようなものが出てくるので、
- 入力Y範囲:1日の平均売上
- 入力X範囲:1日平均乗車人数
- ラベルにチェック(1日の平均売上とかの見出しが含まれているかのチェック)
をそれぞれ選択して、OKを押しましょう。
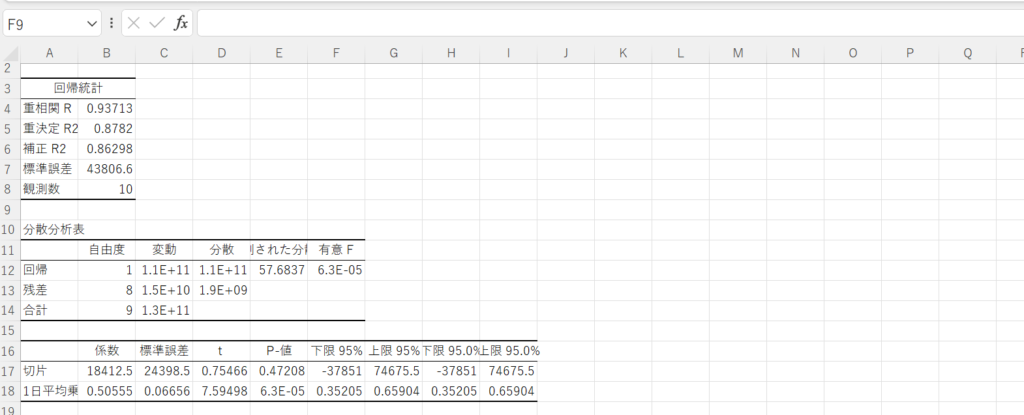
上図のような画面が出てきたら回帰分析は完了で、「係数」が回帰式の部分であり、他にも様々な評価指標が算出されています。
初めのアドインの設定が少し面倒なだけで、一度アドインを入れれば簡単にエクセルでも回帰分析を行えます。
ただし、エクセルは大量のデータを分析するのには向いていないことに注意しましょう。
Googleスプレッドシートでの回帰分析
Googleスプレッドシートでも、回帰分析を簡易的に行えます。
Googleスプレッドシートもエクセルと似たツールであり、多くの人に使われているツールです。
Googleスプレッドシートで回帰分析を行う方法は以下の通りです。
- Googleスプレッドシートにデータを入力する。
- 「挿入」メニューから「グラフ」を選択し、散布図を作成する。
- 散布図に回帰線を追加する。
Googleスプレッドシートでの回帰分析では回帰直線と回帰式の算出までを行います。
まず、表のデータをコピーして、スプレッドシートに貼り付けてください。
そして、貼り付けた表全体を選択し、「挿入ボタン」から「グラフ」を押して、散布図を作成します。
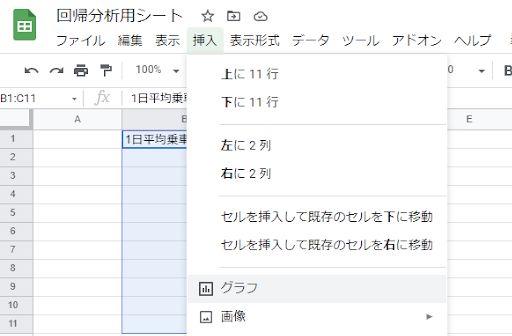
すると下図の散布図が作成されます。

グラフを右クリックし、「系列」から「1日の平均売上」を選択してみてください。
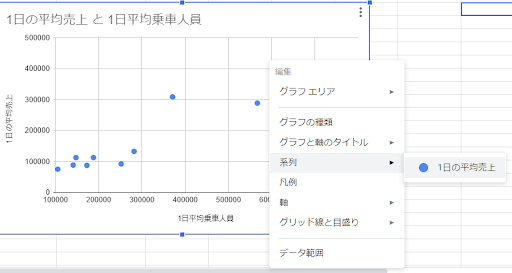
すると下記のような画面が表示されるので、「トレンドライン」にチェックを入れ、「ラベル」で「方程式を使用」を選択します。

下図のようなグラフが表示されていれば回帰分析は完了です。

グラフの上部に回帰式が表示されており、今回の単回帰分析で1日の平均売上と平均乗車人員の関係は
1日の平均売上 = 0.506 × 1日の平均乗車人員 + 18413
であることが見て分かります。
しかし、Googleスプレッドシートでは回帰分析の結果の評価までを行うことができないのが欠点です。
また、エクセルと同様に大量のデータを分析することには向いていないので、以下で紹介するRやPythonを利用することをおすすめします。
Rでの回帰分析
Rは統計解析に特化していて、統計学や機械学習の研究によく使われるプログラミング言語です。
回帰分析は統計学の手法であるため、Rを使って回帰分析が行われることがあります。
Rを用いて回帰分析を行うコードは以下の通りです。
# データの準備 data <- data.frame( 平均乗車人員 = c(789366, 370856, 566994, 281971, 188170, 147699, 252267, 141351, 173003, 105669), 平均売上 = c(407557, 309041, 289068, 133063, 113090, 112910, 92577, 88798, 87856, 75573) ) # 線形回帰モデルの作成 model <- lm(平均売上 ~ 平均乗車人員, data = data) # モデルのサマリー summary(model)
Google colaboratoryでコードを実行すると、以下のように出力されます。
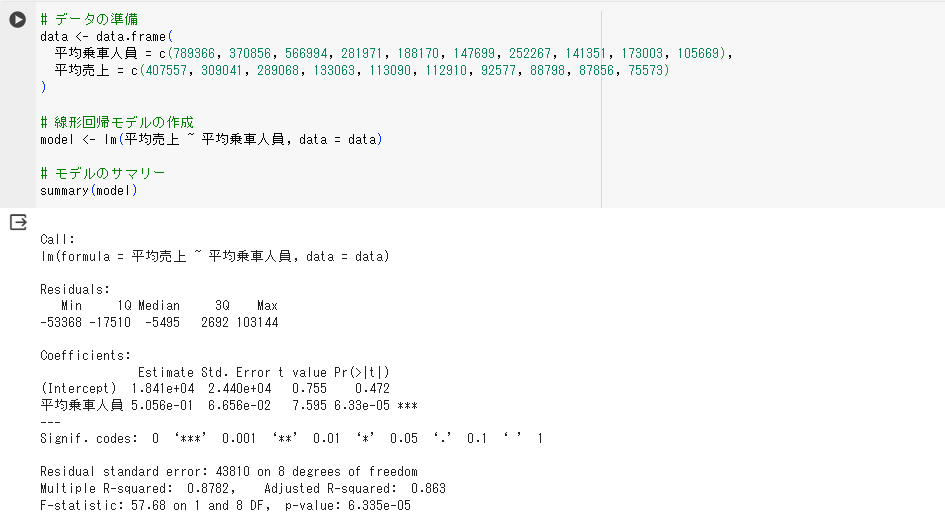
Rは統計解析でよく使われるプログラミング言語ですが、ビジネスシーンでは以下で紹介するPythonの方が利用場面が多いです。
そのため、Pythonでの回帰分析の方法も以下で紹介します。
Pythonでの回帰分析
Pythonは汎用性の高いプログラミング言語で、データサイエンスの分野でも広く使われています。
「Pythonってなに?」と気になる方は、『Pythonとは?3分で分かる人気の理由と基礎知識』の記事をご参照ください。

Pythonで回帰分析を行えるようになることで、回帰分析で現状を把握して他のデータ分析手法でさらに分析を進めることも可能になります。
Pythonで回帰分析を行うコードは以下の通りです。
import pandas as pd import statsmodels.api as sm
# データの準備
data = {
"平均乗車人員": [789366, 370856, 566994, 281971, 188170, 147699, 252267, 141351, 173003, 105669],
"平均売上": [407557, 309041, 289068, 133063, 113090, 112910, 92577, 88798, 87856, 75573]
}
df = pd.DataFrame(data)
X = df[['平均乗車人員']] y = df['平均売上'] X = sm.add_constant(X) # 定数項を追加する # OLS(最小二乗法)モデルの作成 model = sm.OLS(y, X).fit() # 最小二乗法(最適な回帰式)を求める # モデルのサマリーの表示 print(model.summary())
上のコードでは、回帰分析の結果を算出するためにstatsmodelsという統計学のライブラリを使用しています。
PythonのコードをGoogle colaboratoryで実行した結果が下図です。
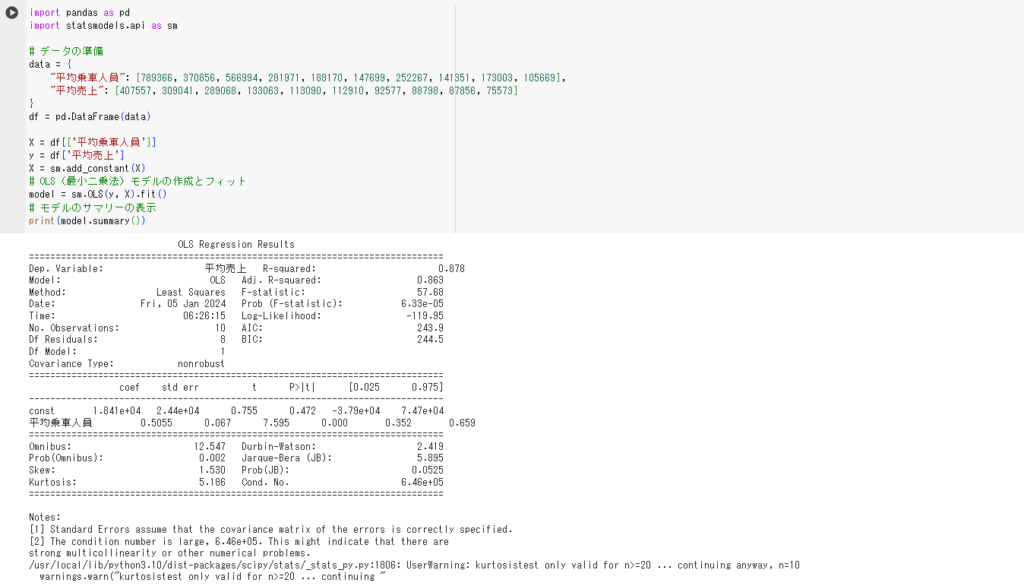
上図のように分析結果を出したい場合は、statsmodelというライブラリを利用することをおすすめします。
しかし、回帰分析を予測に用いる時には、sklearnというライブラリを利用したコードが使われることが多いため、注意しましょう。
以上の4つの方法にはそれぞれ特徴がありますので、あなたの目的や状況に合わせて使う言語を切り替えることをおすすめします。
回帰分析の結果の解釈で見るべき代表的な6つの指標

回帰分析を行って結果を解釈するためには、いくつかの指標を確認しなければなりません。
特に以下の6つの指標は、回帰分析の結果を評価する上で特に重要です。
- 回帰係数:各変数と現状を把握したい変数との相関の大きさ
- 決定係数:モデルの推定値がどれだけ良く当てはまっているか
- 自由度調整済み決定係数:変数の数なども考慮した決定係数
- F値:モデルが統計的に有意か
- t値:各変数が統計的に有意か
- p値:各変数が統計的に有意か(t値より求まる値)
それぞれの指標について、以下で詳しく解説していきます。
【指標1】回帰係数:各変数と現状を把握したい変数との相関の大きさ
回帰係数は、各変数と現状を把握したい変数との相関の大きさを表す係数です。
回帰係数が大きいほど、その変数は現状を把握したい変数(目的変数)と強い関係性があることになります。
回帰係数の正負や値の大きさによって、以下のような判断が可能です。
- 正の値:変数が増加すると、目的変数も増加する。
- 負の値:変数が増加すると、目的変数は減少する。
- 値が大きい:その変数と目的変数との関係性が強い。
- 値が小さい:その変数と目的変数との関係性が弱い。
回帰係数を見ることで、どの変数が目的変数とどれだけ関係性があるのかを把握できます。
ただし、回帰係数の大きさだけで関係性を判断しすぎないようにしましょう。
【指標2】決定係数:モデルの推定値がどれだけ良く当てはまっているか
決定係数は、回帰モデルの予測がどれだけ良く当たっているかを示す指標です。
0から1の間の値をとり、1に近いほどモデルの推定値が正確に当てはまっていると考えてください。
決定係数は以下の式で求められます。
\[ R^2 = 1 – \frac{\sum_{i=1}^{n} (y_i – \hat{y_i})^2}{\sum_{i=1}^{n} (y_i – \bar{y})^2} \]
それぞれの変数の意味が、
・\( y_i \):目的となる変数の値
・\( \hat{y_i} \):目的となる変数の予測した値
・\( \bar{y} \):目的となる変数の値の平均
であり、1 – の後の分数の分母と分子はそれぞれ、
- 分子:予測値と実際の値との差の二乗の合計
- 分母:実際の値の分散
となり、決定係数が求められます。
しかし、決定係数が良い値であるからといって、予測が正確であると決めつけないようにしましょう。
あくまで、1つの評価指標であると捉えておくことが重要です。
【指標3】自由度調整済み決定係数:変数の数なども考慮した決定係数
調整済み決定係数は、関係性を見たい変数の数も考慮した決定係数になります。
多くの変数を回帰分析に使うほど決定係数も高くなる性質がありますが、変数の数が多すぎると他のデータで同じ回帰式を使っても精度が上がらない現象が発生してしまうのです。
そのため、以下の式のように変数の個数を考慮したのが自由度調整済み決定係数になります。
\[ R^2_{\text{adj}} = 1 – \frac{\frac{\sum_{i=1}^{n} (y_i – \hat{y}_i)^2}{n – k – 1}}{\frac{\sum_{i=1}^{n} (y_i – \bar{y})^2}{n – 1}} \]
kが変数の数を示して、nがデータの数であり、決定係数の式と似ていることが見て取れます。
回帰分析の結果の解釈では、自由度調整済み決定係数が示されていることも多いため、決定係数との違いとともに覚えておくことをおすすめします。
【指標4】F値:モデルが統計的に有意か
F値は各変数のうちのいずれかが、統計的に有意であるかを判断するための指標です。
F値が大きいほど、回帰モデルとしての有意性が高く、回帰モデルが現状を把握したい変数をしっかりと説明できていることになります。
F値の計算は以下の通りです。
\[F = \frac{\frac{{\sum_{i=1}^{n} (\hat{y}_i – \bar{y})^2}}{{k}}}{\frac{{\sum_{i=1}^{n} (y_i – \hat{y}_i)^2}}{{n – k – 1}}}\]
ただし、F値は回帰モデル全体の有意性を示すものであり、個々の変数についてはt値やp値を見て、判断する必要があります。
【指標5】t値:各変数が統計的に有意か
t値は、各変数が統計的に意味があるのかどうか(有意か)を示す指標です。
t値が高いほど、その変数と現状を把握したい変数との関係性が統計的に意味があることになります。
回帰分析におけるt値は以下の式で表せます。
\[ t = \frac{回帰式の各変数の係数 \times \sqrt{データの個数}}{標準偏差} \]
以上の式でt値を求めることで、各変数がどれほど現状を把握したい変数と関係性があると言えるのかを把握できます。
【指標6】p値:各変数が統計的に有意か(t値より求まる値)
p値もt値と同様に各変数がどれだけ統計的に有意かを示す指標です。
通常、p値が0.05以下であれば、変数は統計的に有意とみなされます。
p値が低い場合、以下のことが言えます。
- 変数は目的変数に対して統計的に有意である可能性が高い
- 目的変数との関係性は偶然ではない可能性が高い
p値は標準化した正規分布やt値から求められますが、回帰分析の結果の解釈ではとりあえずp値が0.05以下であれば良い可能性が高いと考えておきましょう。
とはいえ、p値がどれだけ低ければ有意であるとみなすかは、データ分析によって変わるため、注意が必要です。
回帰分析をする際の4つの注意点

回帰分析を行う際、特に注意すべき4つのポイントがあります。
以下に挙げる4つの注意点を把握しておくことで、間違った分析を行う可能性を減らせるので、必ず押さえておきましょう。
- 過学習が起こる可能性がある
- 多重共線性が起こる可能性がある
- データに外れ値があるかもしれない
- 因果関係が分かるわけではない
それぞれの点について詳しく解説していきます。
過学習が起こる可能性がある
過学習はモデル(回帰分析でいう回帰式)が訓練データ(回帰式を求めるために利用したデータ)に対して過剰に適合してしまう現象です。
回帰分析などで予測を行う場合には、以下のようにデータを2つに分割します。
- 訓練データ:モデル(回帰式など)を求めるためのデータ
- テストデータ:モデル(回帰式など)が本当に正確なのかを調べるためのデータ
しかし、回帰分析で変数(分析に用いる項目)の数が多くなりすぎると、偶然起きていることについても過剰に反応してしまうことがあります。
なので、予測なども行う回帰分析では、偶然の影響をできるだけ抑える汎用的なモデル(回帰式)を作成することを心がけましょう。
特に、重回帰分析では変数の数を多くしすぎないように意識することをおすすめします。
多重共線性が起こる可能性がある
回帰分析では、目的変数以外で変数(項目)間に強い相関関係がある時に多重共線性が起こる可能性があります。
多重共線性とはある変数と他の変数との間に強い相関がある状態で、多重共線性が発生しているとある1つの特徴に偏った回帰分析になってしまう可能性があるのです。
多重共線性が起きているかどうかは、以下の点から判断できます。
- 変数間で相関関が強いところがある
- ある1つの特性に偏っている
例えば、生徒の成績を把握したい時に、以下の2つの変数は多重共線性が起きている可能性があります。
- 授業の出席回数
- 宿題の提出回数
授業に出席している学生は基本的に宿題もしっかりと提出していることが考えられ、2つの変数の間には相関がある可能性が高いです。
このような場合に、多重共線性が発生してしまい、「授業」または「宿題」のどちらか一方のみ、目的変数との関係が見られる回帰式になってしまう可能性があります。
多重共線性を回避するには、相関の高い変数間のどちらかを除外するなどの対処を行うことをおすすめします。
データに外れ値があるかもしれない
外れ値があると回帰分析を行う場合に大きな影響があるため、注意が必要です。
外れ値とは一般的なデータの群から大きく離れた値のことで、回帰式を求める時に誤差が大きくなることを防ごうとしてしまうため、外れ値に寄った式を求めてしまいます。
外れ値を確認するためには、以下のような方法で確認しましょう。
- 散布図で可視化する
- 箱ひげ図から見つける
箱ひげ図について詳しく知りたい方は『箱ひげ図を使うメリット・デメリットや実際の作り方を解説』の記事をご参照ください。
例えば、年収の状況を把握したい時には、飛びぬけて高年収の人が外れ値に当たります。
外れ値の影響を抑えるには、外れ値を見つけて取り除くか、外れ値の影響を受けにくい手法を使用することをおすすめします。
因果関係が分かるわけではない
回帰分析は相関関係を示すもので、因果関係を証明するものではないことにも注意しましょう。
回帰分析の結果、現状を把握したい変数に対して関連性がある変数を見つけられたとしても、因果関係までは分かりません。
例えば、生徒の成績を把握するために回帰分析を行って、勉強時間が関係していると分かったとしても勉強時間を増やせば成績が上がるとは断定できないのです。
- 勉強時間が多いから成績が良い
- 成績が良いから勉強時間が多い
以上のように、どちらの因果で関係性があるかまでは分からないため、回帰分析はあくまで関係性までを把握するためであると考えましょう。
関係性があることを因果関係があると勘違いしてしまうことが多いため、回帰分析を行う際は注意しておくことをおすすめします。
まとめ
回帰分析とは現状の傾向を把握したい変数について他の変数との関係を数式で表す統計学の分析手法です。
代表的な回帰分析の手法は以下の3種類になります。
- 単回帰分析
- 重回帰分析
- ロジスティック回帰分析
変数の数や現状を把握したい変数が数値か数値でないかなどで回帰分析の種類を変える必要があります。
現在、回帰分析は現状の傾向の把握の把握に用いられ、予測を行う場合は他のデータ分析手法が用いられることが多いです。
回帰分析を使った現状の傾向の把握は、以下のようなところに活用されています。
- 現在の売上状況の把握
- 現在の需要の傾向の把握
- 不動産価格の決定
以上の例以外にも、現状の傾向の把握を行いたい時に回帰分析が用いられます。
現状の傾向を把握する際には、以下の手順で回帰分析を行いましょう。
- 【STEP1】現状を把握したい項目とその関係性を見たい項目を選ぶ
- 【STEP2】回帰分析を行う
- 【STEP3】回帰分析の結果を解釈する
これらのステップに沿って分析を進めることで、効果的に回帰分析を行えます。
また、回帰分析の結果を解釈する時には、以下の指標に注目しましょう。
- 指標1】回帰係数:各変数と現状を把握したい変数との相関の大きさ
- 【指標2】決定係数:モデルの推定値がどれだけ良く当てはまっているか
- 【指標3】自由度調整済み決定係数:変数の数なども考慮した決定係数
- 【指標4】F値:モデルが統計的に有意か
- 【指標5】t値:各変数が統計的に有意か
- 【指標6】p値:各変数が統計的に有意か(t値より求まる値)
以上の指標を理解して適切な解釈を行うことで、現状の傾向の把握を行えます。
しかし、回帰分析を行う際には多くのことに注意する必要があり、”正確に”現状の傾向の把握を行うのは大変難しいです。
もし、「正確に現状の傾向を把握したい」「現状の傾向から未来を予測したい」とお悩みであれば、『Caccoのデータサイエンス』にご相談ください。
詳細は以下のバナーをクリックの上、ページをご参照ください。