「ロジスティック回帰分析ってどうやってやるの?」
「ロジスティック回帰分析をしたはいいけど、どうやって活用するの?」
とお悩みではありませんか?
ロジスティック回帰分析は2値の分類を行え、分類の中で重要な変数について抽出する手法です。
分類を予測できるだけでなく、影響を与えた重要な変数を見つけ出せることでサービスなどの改善点や重要視すべき点を客観的に判断できます。
本記事では、
- ロジスティック回帰分析を使える場面
- ロジスティック回帰分析の手順
- ロジスティック回帰分析の実装
についてお伝えしていきます。ぜひ参考にしてみてください。
ロジスティック回帰分析とは
ロジスティック回帰分析は2値に分類する手法です。
ロジスティック回帰分析を行うことで、商品が売れるかどうか、サービスを継続してくれるかどうかなど「はい」か「いいえ」で知りたい情報を予測できます。
以下で解説していきます。
そもそも「2値に分類する」とは?
2値に分類するとは「はい」か「いいえ」に分類することです。
ロジスティック回帰分析は、商品が売れるか売れないか、サービスを継続してもらえるかしてもらえないか、などさまざまな「はい」か「いいえ」の問題を予測できます。
映画サービスの継続してもらえるのかの分析の例で説明していきます。

この分析で知りたい情報は、ユーザが1か月以上サービスを継続するかどうかです。
先ほどの「はい」と「いいえ」に置き換えてみると、
- はい:サービスを継続する
- いいえ:サービスを継続しない
となります。
ロジスティック回帰分析は、「はい」か「いいえ」で答えられるように目的となる変数を決めることで課題を解決する手法です。
ロジスティック回帰分析でできる2つのこと
この章では、ロジスティック回帰分析でできる2つのことについて解説していきます。
ロジスティック回帰分析を行うことで、以下の2つのことができます。
- 事象の説明や解釈を行える
- 予測を行える
今起きている事象を解釈するために用いるのか、さらに将来の予測まで行うのかの2つです。
それぞれ解説していきます。
事象の説明や解釈を行える
ロジスティック回帰分析は、ある事象がなぜ起こっているのかの解釈を行うのに役立ちます。
何かアクションを起こすにも、現状を正しく把握している必要があり、そのような場合の事象の理解にロジスティック回帰分析が用いられるのです。
例えば、学生が大学に合格するのに何が必要かを把握したい場合、考えられる各変数(テストスコア、勉強時間、部活動の参加など)が合格とどれくらい相関があるか調べられます。

上図のように、それぞれの要因がどれだけ大切であるのかを客観的に理解するために、ロジスティック回帰分析が必要なのです。
また、以下で説明する「予測を行う」の場合にも、まず現状の把握や解釈から行うため、事象の説明や解釈はロジスティック回帰分析で必ず行うことになります。
予測を行える
ロジスティック回帰分析は、予測を行うために広く利用されています。
特に、ロジスティック回帰分析は、2つのカテゴリ(合格/不合格、購入/非購入など)での、事象が発生する確率を予測するのに用いられます。
例えば、顧客がある商品を購入する確率を予測するかどうかを予測する際にロジスティック回帰分析が利用されます。
上図のように、顧客の年齢、購買履歴、クリック履歴などの情報から、購入確率を予測し、マーケティング戦略を最適化できます。
このように、ロジスティック回帰分析を用いることで、事象の発生確率を予測し、効果的な戦略を立てられるのです。
以下では、事象の説明や解釈も含めたロジスティック回帰分析を用いた予測について解説していきます。
ロジスティック回帰分析で予測できる4つの例
この章では、ロジスティック回帰分析で予測できる具体的な例を紹介していきます。
2値分類を行って要因となる変数も特定できるため、ビジネスを始めとして多くの分野で利用可能です。
今回は、代表的な以下の4つの例を紹介します。
- 商品の購買予測
- サブスクリプションサービスの継続予測
- 病気の予測
- 不正の検知予測
それぞれ解説していきます。
商品の購買予測
ユーザの行動データを元にロジスティック回帰分析を用いて商品の購買予測を行えます。
ECサイトは毎日多くのユーザが購買行動を起こしているため、もととなるデータの宝庫です。
キャンペーンによってどれだけ購買が促進されたのか、ある商品を買っている人は特定の商品を買っているなどを分析できます。
サブスクリプションサービスの継続予測
ユーザがサブスクリプションサービスを継続するかしないかの予測にも使えます。
サブスクリプションサービスは継続するかしないかという「はい」か「いいえ」に分かれる問題を設定できるため、ロジスティック回帰分析がしやすいです。
例えば、新しいキャンペーンをする際にどれだけのユーザの継続に効果があるのかなどの効果分析にロジスティック回帰分析を使用できます。
病気の予測
医療では、ロジスティック回帰分析を用いて患者の病気の発症の有無を予測できます。
医療分野では日々、病気の発症の有無がさまざまな変数とともにデータとして蓄積中です。
例えば、ある疾患が発症するかどうかを患者の健康データや生活習慣を参考となる変数(説明変数)をもとに判定できます。
不正の検知予測
ロジスティック回帰分析を用いて不正の検知も予測できます。
不正をしているユーザは、その他一般ユーザと別の行動をしている可能性が高いため、ロジスティック回帰分析で予測できるのです。
顧客の取引履歴やアクティビティのデータを用い、不正のリスクを可視化できます。
ロジスティック回帰分析の手順

ロジスティック回帰分析は以下の5STEPで行います。
- 分析するデータの準備・加工
- データを分析するための環境の設定
- ロジスティック回帰のモデルの作成
- 作成したモデルの予測精度を評価
- 分類を左右している変数(項目)の分析
ロジスティック回帰分析は計算が複雑なため、プログラミング言語などのツールが必要です。
プログラミング言語を動かすための環境設定の方法も含めて、分析の手順を簡単に解説していきます。
STEP1. 分析するデータの準備・加工
データの準備・加工はロジスティック回帰分析にとって重要なステップです。
どのデータであっても完璧なデータは存在せず、事前に分析しやすいように加工する必要があります。
以下のことを確認して加工する作業を行いましょう。
-
- 異常な値のデータはないか
- 抜けているデータはないか
- 単位の異なる数値はないか
- 文字で書かれているデータはないか
異常なデータや抜けているデータがあると、回帰分析を行っても良い精度のモデルにならない可能性があります。
また、単位の異なる数値があれば、値が大きい項目が重視されてしまいます。
例えば、身長と体重では身長の方が大きな値になるため、2つの項目の値の範囲を統一する作業が必要です。
男性や女性などの文字で入力されている項目は、0や1など数値を割り振ることも忘れずに行いましょう。
STEP2. データを分析するための環境の設定
次にデータを分析するための環境を設定します。
ロジスティック回帰分析は数式が複雑であるため、機械での計算が必要です。
今回は機械に指示をするための言語(プログラミング言語)を用いてロジスティック回帰分析を行います。
ロジスティック回帰分析を行うための代表的なプログラミング言語は以下の3つです。
- エクセル
- Python
- R
後半でPythonというプログラミング言語を用いた分析のためのサンプルコードをご紹介しています。
STEP3. ロジスティック回帰のモデル(分類するためのルール)の作成
実行するための環境が整ったら、分析を行っていきます。
まず、データをモデルを作るためのデータ(訓練データ)とモデルを評価するためのデータ(テストデータ)にデータを分割しましょう。
テストデータを訓練データと違うデータにすることで、モデルを作ったデータでなくても良い予測ができるかを判断します。
モデルの作成は、訓練データと実行するための条件をPythonなどのプログラミング言語に用意されている関数(計算式)に入力するだけで終了です。
数万行のデータであっても簡単にモデルを作成できるため、プログラミング言語で分析することをおすすめします。
STEP4. 作成したモデルの予測精度を評価
事前に分割していたテストデータを用いてモデルの予測精度を評価します。
作成したモデルを実際に評価しないで予測に使ってしまうと、実際の結果と全然違う予測をされる可能性があります。
ロジスティック回帰分析では分類の評価指標を用いて評価を行いましょう。
STEP5. 分類を左右している変数(項目)の分析
モデルの評価を終えて予測精度が良いと判断できれば、分類で用いられた項目を分析していきます。
それぞれの項目がどのくらい分類に影響を与えているのかを知ることで、分析対象の強みや弱みを把握できます。
ロジスティック回帰の式から重要な変数を探す
まず、ロジスティック回帰で用いた式を分析していきます。
ロジスティック回帰は以下の式です。
\[ y = ax_1 + bx_2 + \cdots \]
それぞれ以下のように解釈してください。
- \(y\):「はい」か「いいえ」の結果のデータ
- \(x_1,x_2\):それぞれの項目のデータ
- \(a,b\):項目の影響度を表す値(回帰係数)
式の\(a,b\)のような係数(回帰係数)に着目して、項目がどれだけ影響を与えているのかを見ます。
回帰係数だけでも影響度を見れますが、回帰係数を用いてオッズ比を求めることでさらに高度な解釈ができます。
重要な変数が結果にどれだけ影響を与えているのかをオッズ比から計算する
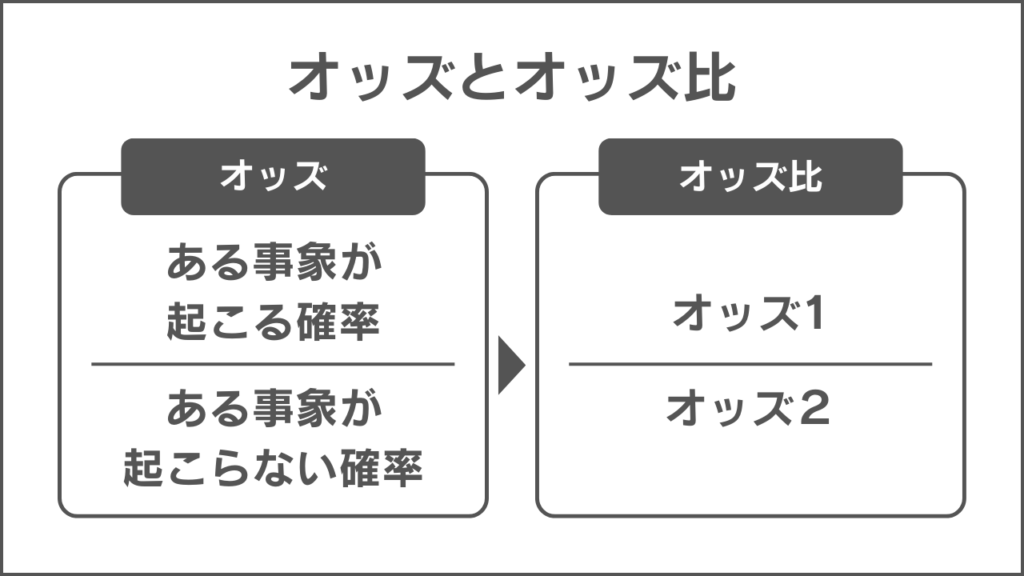
オッズ比を求めることで、あるアクションを起こしているかどうかが最終的な結果にどれだけ結びついているのかを示せます。
先ほどの映画のサービスの継続の例をもとに見ていきましょう。
オッズ:起こる確率 / 起こらない確率
オッズはオッズ比を求める過程で必要となります。
オッズはある事象が起こる確率を起こらない確率で割ったものです。
オッズを求める式は以下の通りです。
\[ オッズ = p \div (1-p) \]
例えば、あるカテゴリの映画を見ている確率が60%だとします。
この場合式に表すと以下の値になります。
\[ オッズ = 0.6 \div 0.4 = 1.5 \]
よって、あるカテゴリの映画を見ているという事象のオッズは1.5と導けます。
オッズ比:オッズ1 / オッズ2
オッズ比はあるオッズに対して他のオッズで割った指標です。
オッズ比を求めることで、ある変数は最終的な結果にどれだけ影響を与えているのかが分かります。
理解しやすいようにあるカテゴリの映画を見る/見ないによるサービスの継続率への影響を例に解説していきます。
| サービスを継続する | サービスを継続しない | |
| あるカテゴリの映画を見る |
80人 |
20人 |
| あるカテゴリの映画を見ない | 40人 | 60人 |
上記の表は、あるカテゴリを見る/見ないによるサービスの継続/不継続の人数を表したものです。
オッズ比は以下のような形で求まります。
オッズ比=
(映画視聴&サービス継続 ÷ 映画視聴&サービス不継続)÷
(映画不視聴&サービス継続 ÷ 映画不視聴&サービス不継続)
分子は映画を視聴した人だけを対象にサービスを継続したかどうかのオッズで、分母は映画を視聴していない人を対象にサービスを継続したかどうかのオッズです。
それぞれの確率は表より求められます。
よって、この時のオッズ比は、
\[ オッズ比 = (0.8 \div 0.2) \div (0.4 \div 0.6) = 6 \]
となります。
オッズ比は1を基準とし、大きいほど良い影響が、小さいほど悪い影響があると判断できる指標です。
オッズ比から、あるカテゴリの映画の視聴はサービスの継続に良い影響を与えている、あるカテゴリの映画を視聴しているユーザは継続しやすいと示せます。
反対に、0.5などで少数の時は継続しにくくしている要因の可能性が高いです。
オッズ比についてより詳しく知りたい方は『オッズ比の使い方』の記事をご参照ください。
また、より詳細にロジスティック回帰分析の結果の解釈について知りたい方は『ロジスティック回帰の結果の見方』の記事をご参照ください。
回帰係数からオッズ比を計算する
さきほど説明した回帰係数が用いるとオッズ比が簡単に計算できます。
実装では回帰係数を算出してからオッズ比の計算を行いましょう。
回帰係数とオッズ比の関係は以下の通りです。
- 回帰係数:\( a,b \)
- オッズ比:\( e^a,e^b \)
e(ネイピア数)の累乗部分に回帰係数を取ることで、オッズ比を算出できます。
今回ご紹介した5STEPを実践することで、ロジスティック回帰分析が行えます。
プログラミング言語を活用すれば簡単に分析できますが、プログラミングを行わなければ分析の難易度は跳ね上がります。
「ロジスティック回帰分析をプログラミングで行うのが難しい!」という方は、『かっこのデータサイエンス』にお問い合わせください!
ロジスティック回帰分析における3つの注意点

ロジスティック回帰分析の行い方を説明しましたが、注意点があります。
ロジスティック回帰分析を行う時に注意すべきことは以下の3つです。
- 多重共線性の可能性
- 過学習の可能性
- データ数を大きくしないといけない
注意点を意識して分析しなければ、分析をもとに行動しても無益になってしまいます。
正しく注意点を把握して、分析に活かしましょう。
1. 多重共線性が発生する
多重共線性とはそれぞれの項目の間に高い相関がある場合に発生する現象です。
多重共線性を無視してしまうと、影響が大きいと判断した変数がすべて同じような意味になってしまいます。
例えば、ある商品の購入有無に年齢と収入を説明変数として用いたとします。
年齢が上がるにつれ、収入が増加する傾向にあることから2つの項目に相関が発生していますよね。
この状態でロジスティック回帰分析を行ってしまうと、相関があるため、どちらか片方だけ影響があるとすれば十分なのに2つも影響が高いという結果になります。
その結果、重要であるはずの他の変数を見つけ出せなくなるのです。
2. 過学習になる可能性がある
過学習はモデルが訓練データに過度に適合しすぎることです。
もし過学習になっていれば、せっかくロジスティック回帰分析を行ったのに、結果をそのデータの場合しか適用できなくなります。
項目(説明変数)の数が膨大であるとき、いろいろな変数から予測されるため細かくなりすぎ、また別の似たようなデータでは全く別の予測になるということも発生しかねません。
3. データ数が大きくなければならない
ロジスティック回帰分析はデータ数が大きい場合に精度の高い結果を得ることができます。
しかし、データ数が少なすぎると、少し特異な値(外れ値)があればその値に予測結果が影響され、正しい結果を得られなくなります。
ある程度データが蓄積した段階で分析を行うようにしましょう。
Pythonを使えばロジスティック回帰分析が簡単になる
ロジスティック回帰分析はPythonで実装できます。
Pythonにはscikit-learnという機械学習ライブラリがあり、そのライブラリを用いてロジスティック回帰分析を実装することが一般的です。
まずscikit-learnをインストールします。(既にインストールしている場合はスキップしてください)
pip install scikit-learn
今回はロジスティック回帰分析のひな型を用意しました。
以下のコードで日本語になっている部分を修正して、利用してください。
必要なライブラリ(関数が多く用意されているデータ)のインポートから、簡単な評価まで行えます。
import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix
# データの読み込み(ここではCSVファイルを仮定します)
data = pd.read_csv('データのファイルパス.csv')
# 特徴量と目的変数を分割
X = data.drop(columns=['目的変数の列名'])
y = data['目的変数の列名']
# 訓練データとテストデータに分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=1)
# ロジスティック回帰モデルの作成と学習
model = LogisticRegression()
model.fit(X_train, y_train)
# テストデータでの予測
y_pred = model.predict(X_test)
# 精度の評価(正解率のみ)
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)
# 混同行列の表示(オッズで出てきた表)
conf_matrix = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(conf_matrix)
# 回帰係数の表示
coefficients = model.coef_[0]# オッズ比の計算
odds_ratios = np.exp(coefficients)
# 項目とオッズ比の表示
print("オッズ比:")
for feature, odds_ratio in zip(X.columns, odds_ratios):
print(f"{feature}: {odds_ratio}")

まとめ
ロジスティック回帰分析は2値の分類において強力な手法です。
ロジスティック回帰分析を行うことで、2値の分類を予測できるだけでなく、どの変数がより強い影響を及ぼしているのかを分析できます。
医療やECサイトだけでなく、多くの業務においてロジスティック回帰分析を行うことで要因分析が可能です。
しかし、多重共線性や過学習などの注意点にも留意しながら、分析を進めてください。
「ロジスティック回帰のような分析を行いたいけど、何から始めればよいか分からない…」という方は、『かっこのデータサイエンス』にお問い合わせください!