「箱ひげ図ってどうやって作るの?」
「箱ひげ図はどうやって活用するの?」
とお悩みではありませんか?
箱ひげ図はデータのばらつき具合を見える化し、複数データの比較に適したグラフです。
カンタンに作れるだけでなく比較も行えることから、データ分析の第1歩目として用いられます。
本記事では、
- 箱ひげ図とは何か
- 箱ひげ図が使える場面
- 箱ひげ図の作り方
についてお伝えしていきます。ぜひ参考にしてみてください。
箱ひげ図とは
箱ひげ図はデータのばらつきを視覚的に表してくれるグラフです。
箱ひげ図は「箱」と「ひげ」で構成されており、データの特徴を一目で判断できます。
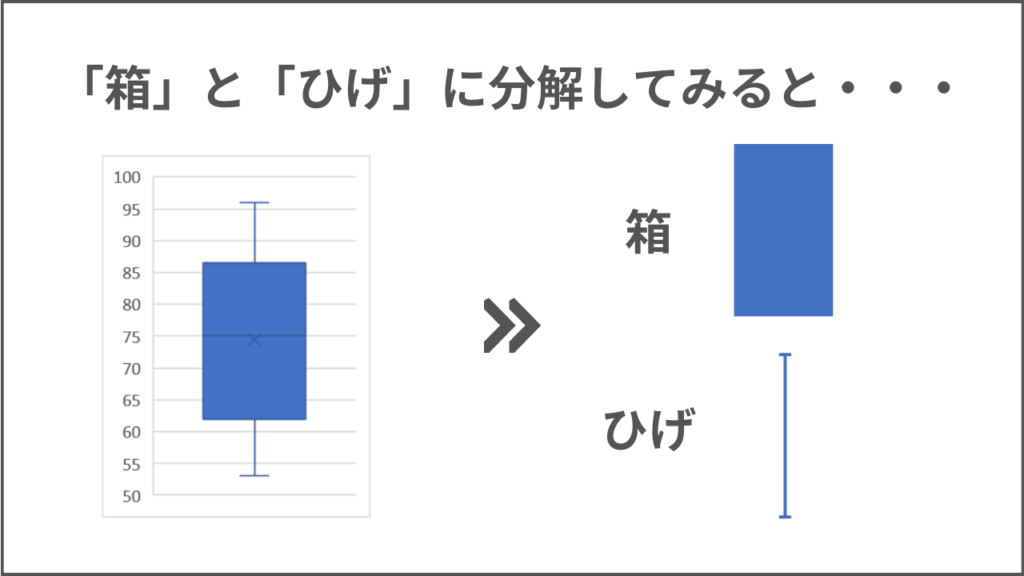
箱とひげに分解すると上記のようなイメージになります。
複数の箱ひげ図を比較することで、違いを見つけ出すこともできます。
箱ひげ図の見方・読み取り方
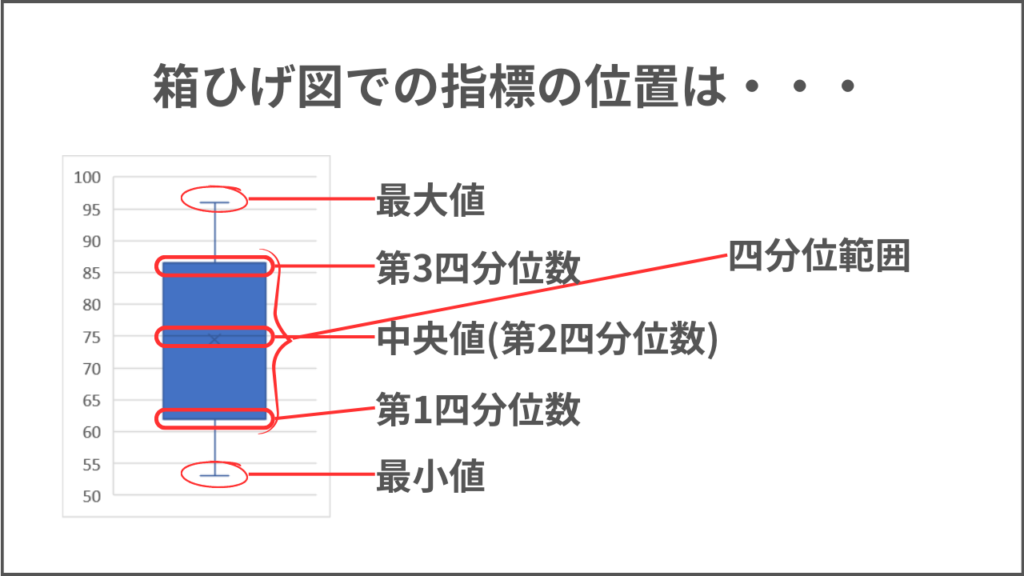
箱ひげ図はデータのばらつき具合を把握するために用いるグラフです。
箱ひげ図を見ることで読み取れる指標は以下の5つです。
- 中央値
- 最小値と最大値
- 四分位数
- 四分位範囲
- 外れ値
これらの値が分かるとデータの分布を把握でき、箱ひげ図を解釈できます。

上の画像のようなデータを例として、わかりやすく解説していきます。
中央値:データの真ん中の値
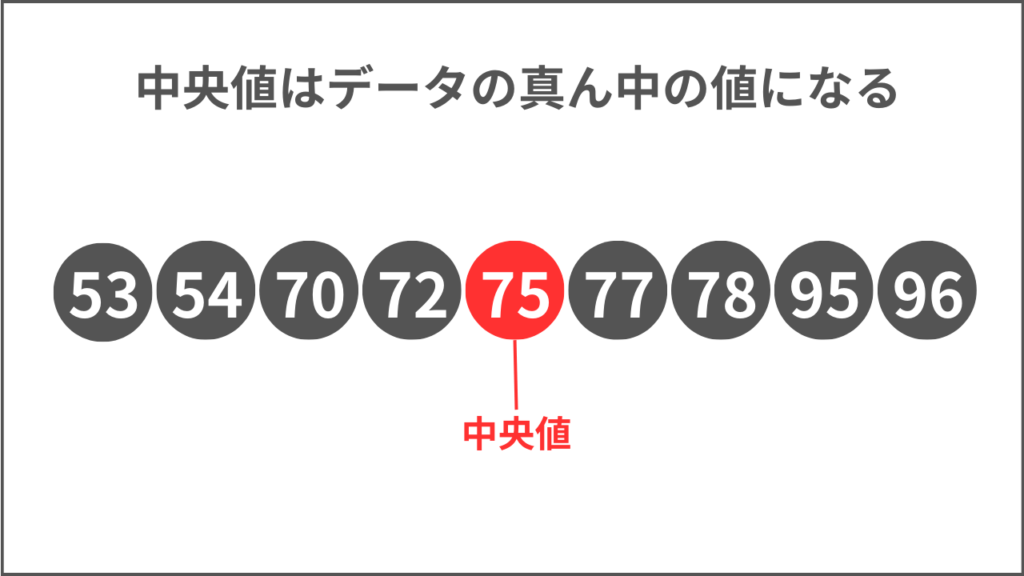
中央値はデータを小さい順に並べたときにデータの真ん中に位置し、例題では75が中央値になります。
箱の中に引かれている線が中央値です。
箱ひげ図はデータが小さい順に並べられたグラフで、中央値はデータのちょうど真ん中の値を示します。
50%の所はどこなのかを把握するのに便利なので、初めに確認しましょう。
最小値と最大値
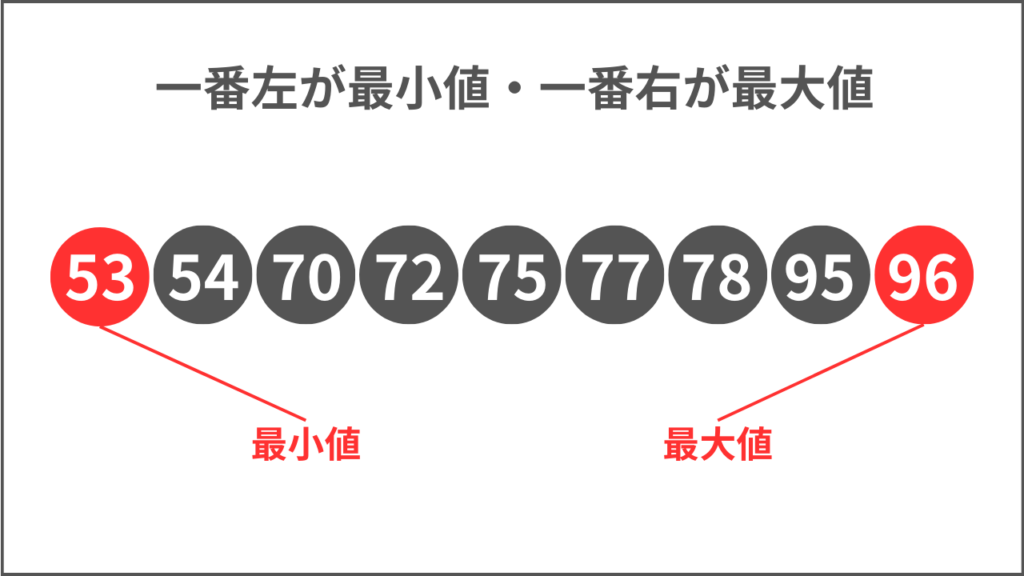
最小値はデータの中で一番小さい値であり、最大値はデータの中で一番大きい値を表します。
ひげの端にある2つの線がそれぞれ最小値と最大値です。
データの範囲がどこからどこまでなのかを最小値と最大値からつかめます。
四分位数:データの区切り

四分位数は、データを小さい順に並べたときにデータを4等分する数値です。
四分位数は箱の両端の線と中央値から構成される数になります。
それぞれを第1四分位数、第2四分位数、第3四分位数と言い、以下のような役割を持ちます。
- 第1四分位数:データの25%の所を示す役割
- 第2四分位数:データの50%の所(中央値)を示す役割
- 第3四分位数:データの75%の所を示す役割
実際に例を用いて3ステップで四分位数を求めてみましょう。
- STEP1 中央値(第2四分位数)を求める
- STEP2 データを2つに分ける
- STEP3 分けたデータでそれぞれ中央値を求める
データを分けて中央値を求めていくことがポイントです。
STEP1. 中央値(第2四分位数)を求める

まず、第2四分位数である中央値を求めます。
ちょうど2等分できる数値が第2四分位数であり、例題だと75が中央値です。
第1,3四分位数を求めるうえで初めに求める値だと覚えておきましょう。
STEP2. データを2つに分ける

中央値(第2四分位数)を求められたら、データを2つに分けましょう。
前半データと後半データに分けることで、それぞれのデータで中央値を求めることで第1,3四分位数を算出できます。
中央値であった数値は含めずにデータを分けましょう。
STEP3. 分けたデータでそれぞれ中央値を求める
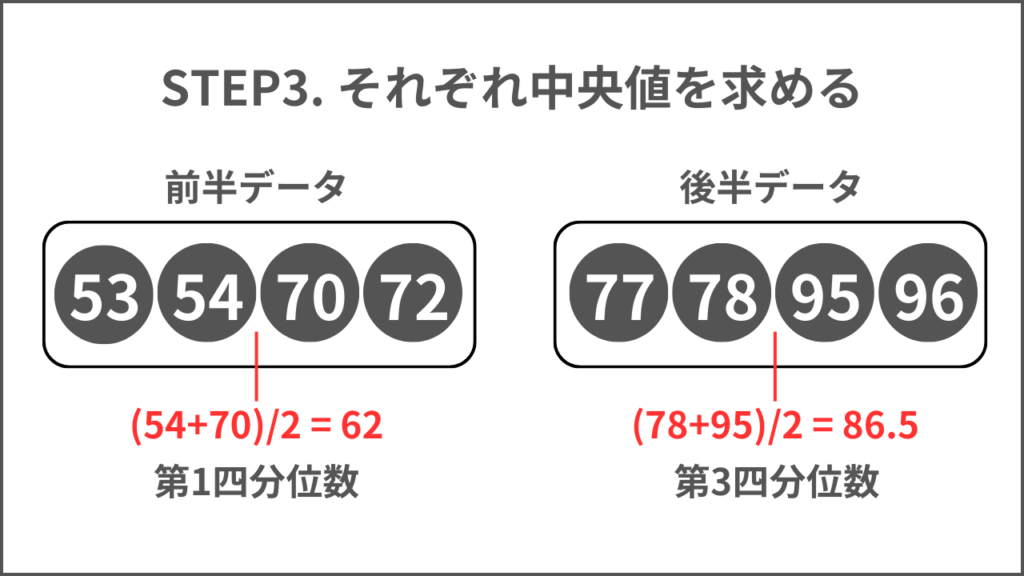
データを2つに分けられたら、それぞれのデータで中央値を求めましょう。
今回はそれぞれのデータが偶数になるので、真ん中2つの値の平均が中央値になります。
例題では、62が第1四分位数、86.5が第3四分位数と算出できました。
四分位範囲:四分位数の範囲を表す
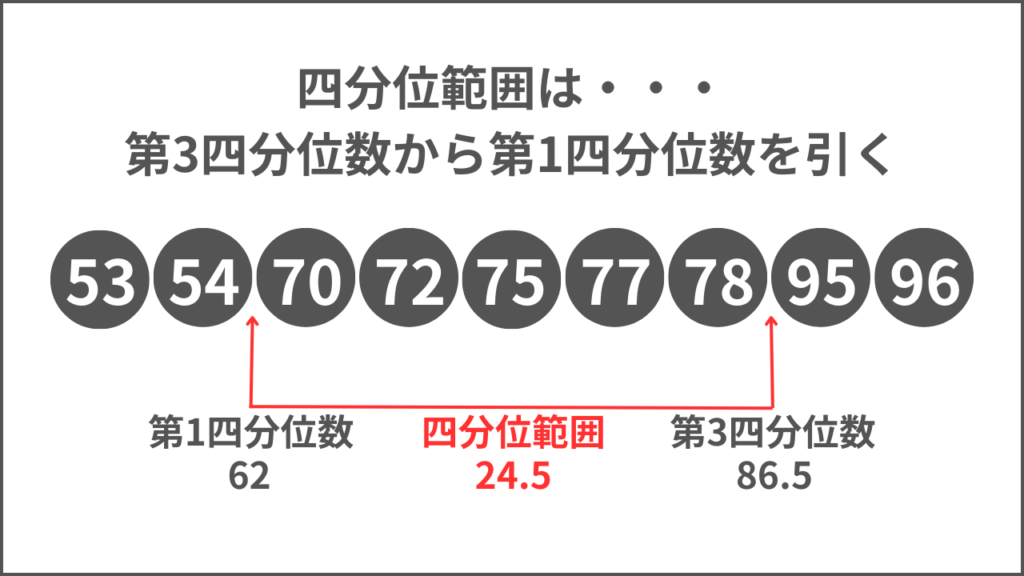
四分位範囲とは四分位数がどれだけの範囲なのかを示す数値です。
箱の長さがそのまま四分位範囲になります。
第3四分位数ー第1四分位数が四分位範囲で、真ん中50%分の値の範囲を把握できます。
例の場合、86.5 – 62 = 24.5 が四分位範囲です。
集めたデータの範囲が広い場合、四分位範囲を求めることで真ん中だけの範囲を知れます。
外れ値:データの分布から外れた値
箱ひげ図でデータの分布から外れて、箱とひげの外に打たれる点が外れ値です。
データの蓄積の際にミスが生じた、たまたま値が極端になってしまったなど様々な場合で外れ値が発生します。
箱ひげ図のひげの両端は、以下の値が上限、下限です。
- ひげの上限:第3四分位数 + 1.5 × 四分位範囲
- ひげの下限:第1四分位数 – 1.5 × 四分位範囲
上記の上限、下限を超えた値が外れ値とみなされてしまいます。
例題では外れ値が出なかったように、相当な値でなければ外れ値になりません。
外れ値が出たときはその値がなぜ出てきたのかを判断して処理することをおすすめします。
箱ひげ図を使うことのメリット・デメリット
箱ひげ図は簡単に計算できる手法ですが、メリット・デメリットがあります。
どの手法にもメリット・デメリットが存在し、正しく把握することで効果的なデータの見える化を行えます。
箱ひげ図でもメリット・デメリットを抑えて、適切に扱いましょう。
箱ひげ図を使うことの3つのメリット

箱ひげ図を使うことのメリットは以下の3つです。
- 複数のデータを簡単に比較できる
- データの特徴をある程度理解できる
- 外れ値を見つけやすい
1つずつ解説していきます。
【メリット1】複数のデータを簡単に比較できる
箱ひげ図を用いることで複数のデータを簡単に比較できます。
1回見るだけで、中央値や最小値、最大値、四分位数を把握できるため、異なるデータと比較することで、データの特徴を比較することに適しているのが箱ひげ図です。
それぞれの商品の購買の年齢層を分析する場合、箱ひげ図で比較することで、どの商品がどの年代によく買われているのかを把握できます。
【メリット2】データの特徴をある程度理解できる
箱ひげ図はデータの特徴を理解することに適しています。
分析したいデータを箱ひげ図でグラフにすることで、データの25%,50%,75%の点や最大値・最小値、外れ値が把握可能です。
四分位範囲が狭いなら、中央付近の値は似たような数字が集まっているのではないかと推測が立てられます。
データを分析するとなったら、まず箱ひげ図でデータの特徴をつかむことをおすすめします。
【メリット3】外れ値を見つけやすい
箱ひげ図は外れ値を見つけやすいです。
外れ値のところで説明しましたが、箱ひげ図では外れ値がひげの外の点として表されます。
外れ値があると分析結果に大きく影響するため、外れ値があるかどうかを把握しなくてはなりません。
まず、外れ値があるかないかを箱ひげ図を使って確認し、その外れ値が意味のあるデータかどうかを判断するようにしましょう。
箱ひげ図を使うことの3つのデメリット

箱ひげを使うことにはデメリットも存在します。
デメリットは以下の3つです。
- 詳細なデータの分布を把握できない
- データの数によって見え方が変わる
- データの比較に注意が必要
こちらもそれぞれ1つずつ解説します。
【デメリット1】詳細なデータの分布を把握できない
箱ひげ図はデータの概要を把握するのに適していますが、詳細な分布は把握できません。
箱ひげ図によって四分位数を把握できますが、四分位数間でどのようなデータの増加が起こっているのかを把握できないのです。
データの概要は箱ひげ図を使って把握し、詳細なデータの分布は別のグラフを使うようにしましょう。
【デメリット2】データの数によって見え方が変わる
データの数の違いによって、箱ひげ図の見え方は大きく変わります。
データの数が少ないと、1つ1つの数値が大きな意味を持ち、データが1つ追加されるだけで箱ひげ図が大きく変わってしまいます。
また、データの数が少ないとデータの幅が狭くなるため、少しでも極端な値を取れば外れ値とみなされることもあります。
データの数を大きくしたほうが箱ひげ図は安定するため、データは多く用意しましょう。
【デメリット3】データの比較に注意が必要
箱ひげ図で複数のデータを並べて比較する時には注意が必要です。
それぞれの箱ひげ図でデータの範囲が極端に異なると適切に分析できない可能性があります。
例えば、身長の分布の箱ひげ図と体重の分布の箱ひげ図を比較するとしましょう。
身長は数値が100を超える分布なのに、体重が50台の分布になるため、体重のほうが低い値の分布だと決めつけてしまいます。
2つの違いは単位です。
必ず単位をそろえること、単位がそろっていても極端に値に分布が違う場合は注意しましょう。
箱ひげ図が使える3つの場面

箱ひげ図は複数のデータを比較するのに便利です。
この記事では以下の3つの例を取り上げます。
- 複数ジャンルの商品の売上分析
- 顧客の分析
- 物件選び
これらの例は箱ひげ図だけで分析できるため、ぜひ取り入れてみてください。
複数ジャンルの商品の売上分析
複数ジャンルの商品の売上分析に箱ひげ図が使えます。
複数のジャンル(業態)を運営している企業などで複数のジャンルの売上を見える化するなら、箱ひげ図を使いましょう。
どのジャンルが今売り上げを伸ばせているのか、どのジャンルが伸びていないのかを一度に把握でき、次のビジネスプランを考えられます。
顧客の分析
顧客の分析にも箱ひげ図が便利です。
売上のもととなる顧客を理解することはビジネスを行う上で不可欠で、データを用いて客観的に顧客の理解を進めなくてはなりません。
それぞれの商品ごとや来店頻度ごとで年齢層を見える化することで、自社の商品はどの年齢層に人気なのかを把握できます。
物件選び
物件選びでも箱ひげ図を利用できます。
物件を探すとなると、どの駅に住むべきか、家賃はどのくらいの幅があるのか、などさまざまなことを考えなければなりません。
箱ひげ図を用いることで、駅ごとの家賃の分布を比較できます。
それぞれの駅の家賃の分布をおおまかに把握できれば、どの駅なら家賃が安い傾向にあるのかなどを知れます。
実際に家賃の分析を行った例を知りたい方は『箱ひげ図 について超カンタンに解説してみた』の記事をご参照ください。
箱ひげ図はExcel(エクセル)で作れる
箱ひげ図はExcelで簡単に作れます。
エクセルを使って、以下の4ステップで箱ひげ図を簡単に作成します。
- STEP1 データを用意する
- STEP2 データを選択する
- STEP3 挿入タブ>統計データの挿入をクリック
- STEP4 装飾を整える
1つずつ説明していきます。
STEP1. データを用意する
まず、箱ひげ図で見える化したいデータを用意します。
手元に何もデータがないという方は、=RANDBETWEEN(最小値の値,最大値)とセルに入力して乱数でデータを作りましょう。
今回は、商品Aと商品Bでそれぞれの購入者50人の年齢層の分布を比較する例で解説していきます。
各商品の乱数を作成するコードは以下の通りです。
- 商品Aのコード:=RANDBETWEEN(20,70)
- 商品Bのコード:=RANDBETWEEN(40,60)
STEP2. データを選択
作成したデータをすべて選択します。
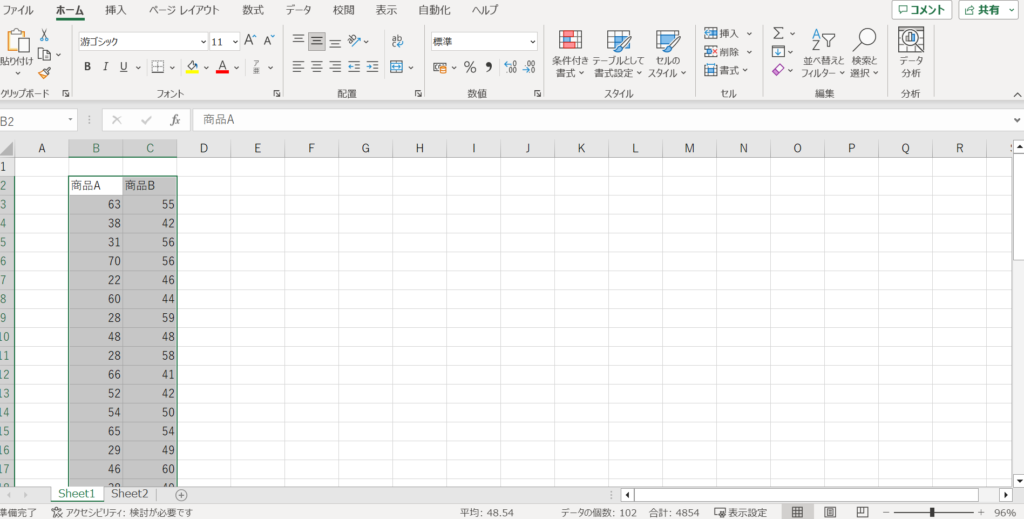
上の画像のように選択してください。
STEP3. 挿入タブ>統計データの挿入をクリック
データを選択している状態のまま、挿入タブから統計データの挿入をクリックします。
挿入タブをクリックすると以下のような画面になります。

黄色の枠で囲っているところにマウスのカーソルを合わせると「統計データの挿入」と出てくるのでクリックして、箱ひげ図をクリックしてください。
以下のような画面になれば成功です。
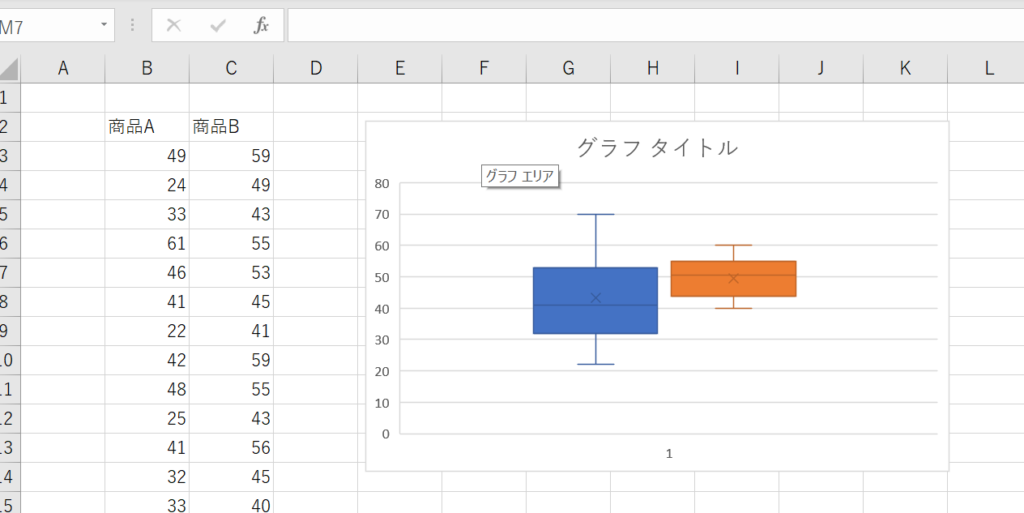
STEP4. 装飾を整える
グラフを見やすくするために、タイトルや軸、凡例(データのラベル)の追加などを行います。
タイトルの変更は「グラフタイトル」と書いてあるところをクリックし編集していきます。
仮として商品Aと商品Bの年齢層比較とタイトルを書きましょう。
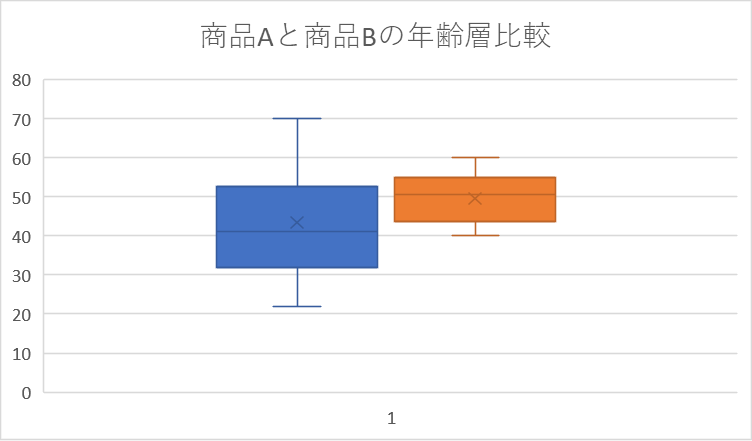
今のままだと少し箱ひげ図が小さくなってしまっているので、軸の目盛りを変更していきます。
目盛りが書いてあるところを選択して右クリックすると以下のような画面になるので、目盛線の書式設定をクリックします。
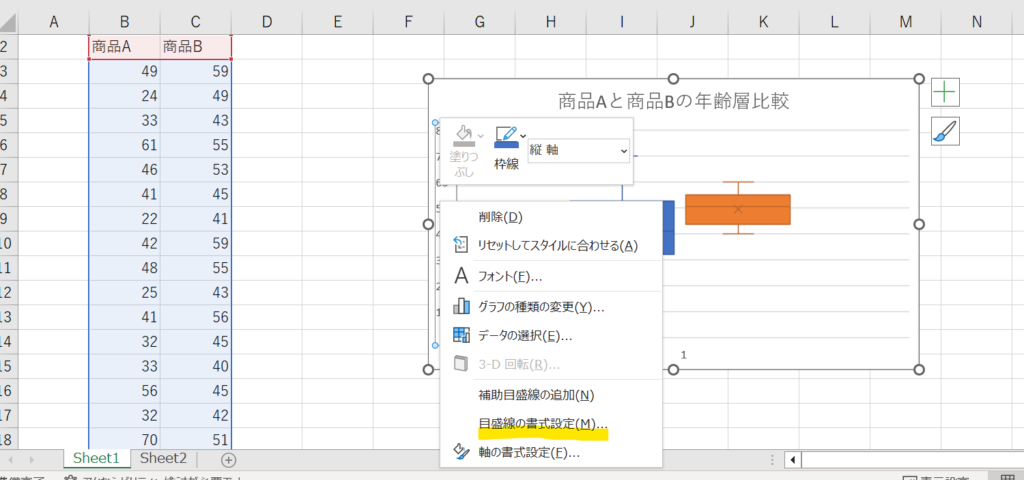
すると右側に軸の書式設定と出てくるので、最小値を10に変更してみます。
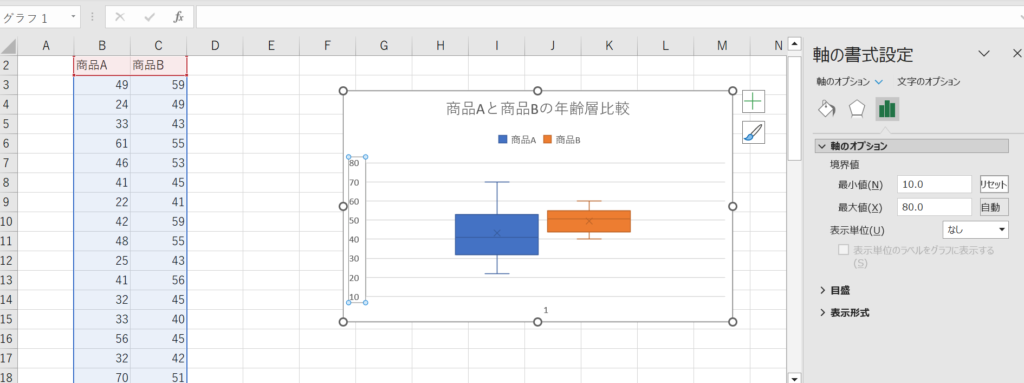
最後は凡例(データのラベル)の追加です。
グラフを選択して右側に表示されている+マークをクリック、凡例にチェックを入れてください。
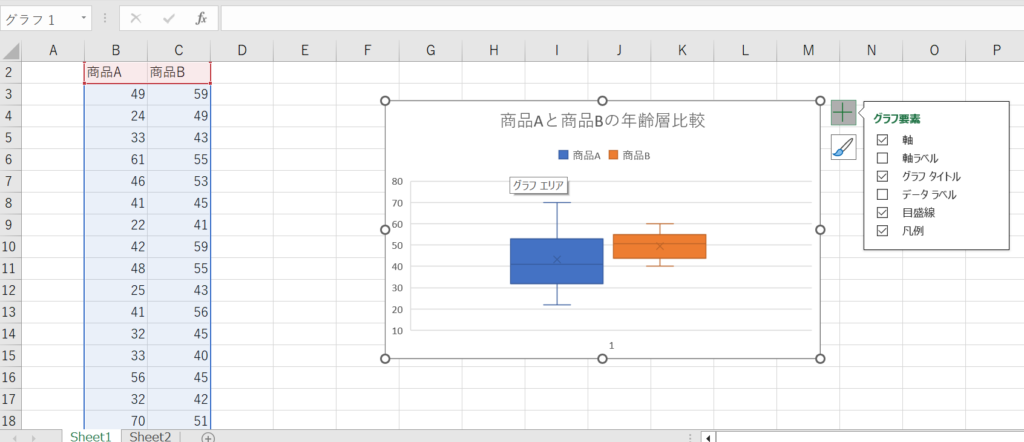
上記のように商品Aと商品Bという文字が表示されたら、箱ひげ図の完成です。
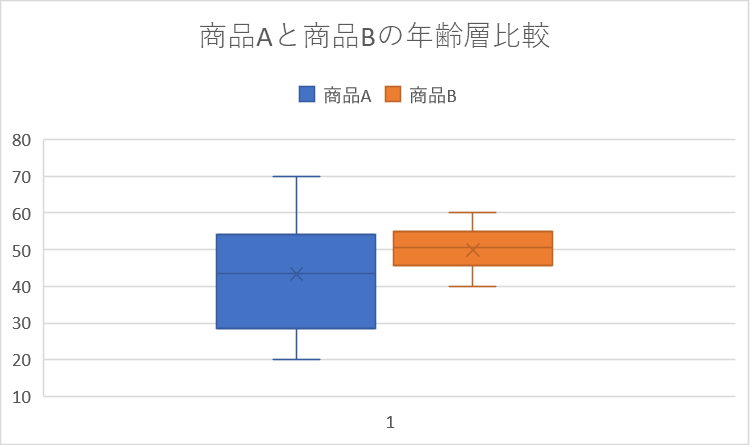
今回の例では、商品Aより商品Bの方が購入者の年齢層の幅が狭いと分かりました。
もし、私がアパレル事業者でこの箱ひげ図の分析の結果を用いるのなら、「50代付近の年齢層をターゲットに商品Bを売り出すキャンペーン」を新たに考え、社内に提案します。
このように、箱ひげ図だけでも重要な情報を手に入れることができるので、あなたの手元にあるデータでも上記のステップを使って箱ひげ図を作成してみてください。
まとめ
箱ひげ図はデータの特徴や分布を把握するのに便利なグラフです。
複数のデータを比較したり、外れ値を見つけることができ、エクセルで簡単に作れます。
しかし、詳細なデータ分析には向いていないため、データ分析の最初の段階であるデータの特徴を把握することに利用しましょう。
「さらに高度なデータ分析を行いたいけど、やり方がわからない」という方は以下のバナーをクリックの上、『かっこのデータサイエンス』にお問い合わせください。